Last summer, my friend and math teacher extraordinaire Peg Cagle started teaching me to knit. It’s been wonderful — something I can do while listening to audiobooks. I’ve been trying to push myself a little bit each time I pick a new project [1]. I’m now working on something called the Boneyard Shawl by Stephen West (who is one of my favorite knitting designers). This is what the final shawl looks like:

Now I was at the library knitting, after writing a college recommendation and needing a breather… and I started wondering seeing some nice math in what I was doing. So I wanted to recreate some of that thinking here and extend it.

Before starting, you should know how it is knit. Here’s what I had at the library:

The way this is knit isn’t across the top like you’d think. No, in fact, you go along the triangular edge, from the left side to the apex to the right side — like the yellow lines I added in show. Then you flip it over and do a basic stitch on the back the entire way. So you’re doing two rows of stitches, one row on the front, one row on the back. So to finish “one full” repeat of the shawl, you go back and forth along the triangle. The four places with DOTS are special places. where you ADD a new stitch the first time you stitch across the triangle, and then you “lock in” those stitches when you stitch across the back. So in total, for each back-and-forth, for every two rows, you’re adding in a total of four new stitches.

And that makes sense — you have to add stitches every two rows — because your triangle is getting bigger!

I then did some counting of my stitches, and found the following:

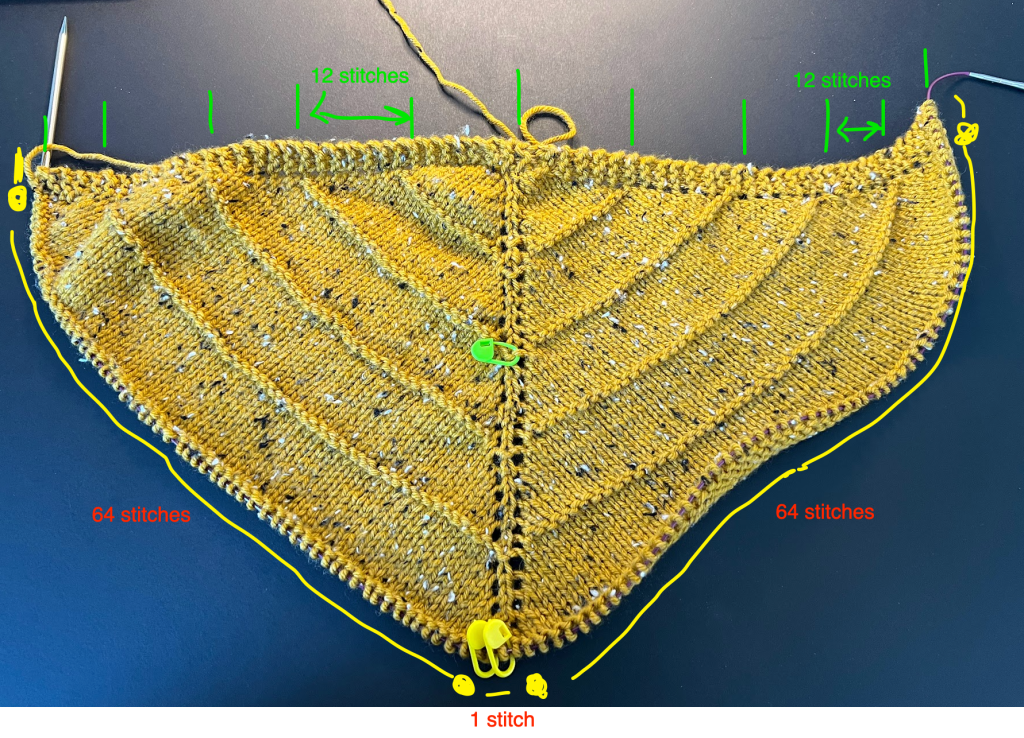
I saw I had 64+1+64 stitches for where I was at in my knitting process.

I also noticed that I was on my 60th row of knitting. (The top measures how many rows I’ve knit… And from the center, I have 12*5=60 stitches.)

For my 59th and 60th row of knitting, I had 64+1+64 stitches.

So for my 61st and 62nd row of knitting, I’d have 68+1+68 stitches (remember I add 4 stitches every other row)

For my 63rd and 64th row of knitting, I had 72+1+72 stitches.

I love that I see an arithmetic series here! So I came up with this gem!

And indeed, it works!

So for row n we have this many stitches:

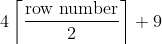
Now. Okay, let’s make things easier and only use even row numbers… then we get 2(row number)+9.

An obvious question for me is: how many stitches will be in this whole thing?

Well, looking at the original grey Boneyard Shawl picture, I see we have 14 triangles, and then a simple border.

Let’s ignore that simple border and only consider the 14 triangles. Each triangle requires 12 rows of knitting! So at the end, we’ll have done 14*12=168 rows.

In the last row, we’ll have 2(168)+9=345 stitches

So we have row1+row2+row3+row4+…+row167+row168 stitches.

This is 13+13+17+17+…+345+345

There are many ways to add up this arithmetic series. I get 30,072.

To find the sum to an even number of rows, let’s say we want to add up to row n. Then we have a total number of stitches of:

Whoa! It simplifies nicely!

When I’m knitting, I think about each set of 12 rows as one “triangular section.” And obviously, each set of 12 rows takes longer to knit than the previous set since there are more stitches. Let’s figure out how many more!

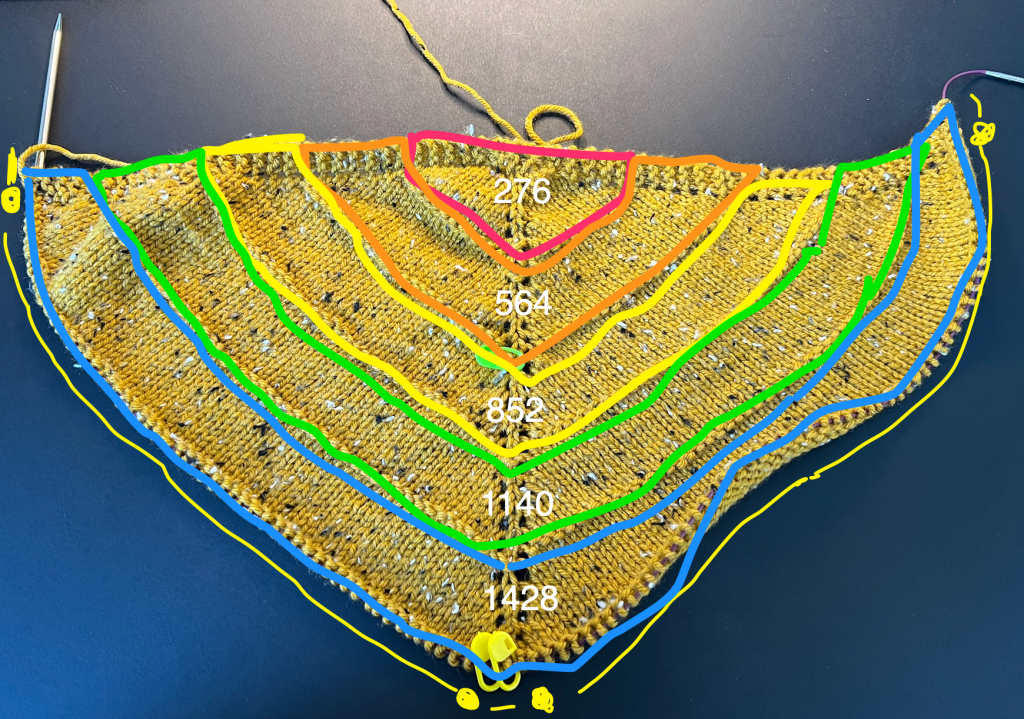
I wanted to see how much longer each section would take to knit than the section before. Each stitch takes about the same amount of time, so the second triangular section would be 564/276=2.04 times longer… Looking at the chart, we see:

And this makes sense to me. Although each section is taking longer to knit than the previous section, as we get near the end that ratio gets closer and closer to 1. This is because we’re only adding a fixed 288 stitches each time we create a new section, compared to the previous section.

And of course since the number of stitches in the first section is so small that adding 288 to that is a relatively large proportion of stitches,, while the number of stitches in the final sections are so large that adding 288 to that is a relatively small proportion of stitches.

Okay, let’s now get to time! I did a quick test of my knitting and it takes me about 4.651 seconds on average per stitch.

For the whole shawl it will take me:

30,072 stitches * 4.651 seconds / stitch * 1 hour / 3600 seconds = 38.85 hours.

But as I’m knitting, I think in terms of each triangular section. It’s too daunting to think in terms of the whole thing. So this is how much time it will take me-ish to do each section:

Okay. As I was doing all of this, I saw so many connections to calculus… derivatives and integrals! Maybe I’ll blog about that at some point… but hopefully you can see hints of those things popping up.

UPDATE: I wrote a quick followup for the blogpost showing some of the calculus connections: Knitting Math — Part II

[1] If you’re wondering… I’m really enjoying knitting this! It’s my first shawl, and I thought the pattern looked a little too advanced for me. In fact, it is the perfect first shawl! Stephen West has a tutorial video here. I’d say if you’re thinking of tackling a shawl, this is a great one to tackle!