This is a continuation of the previous post. My goal here is to connect this up to calculus.

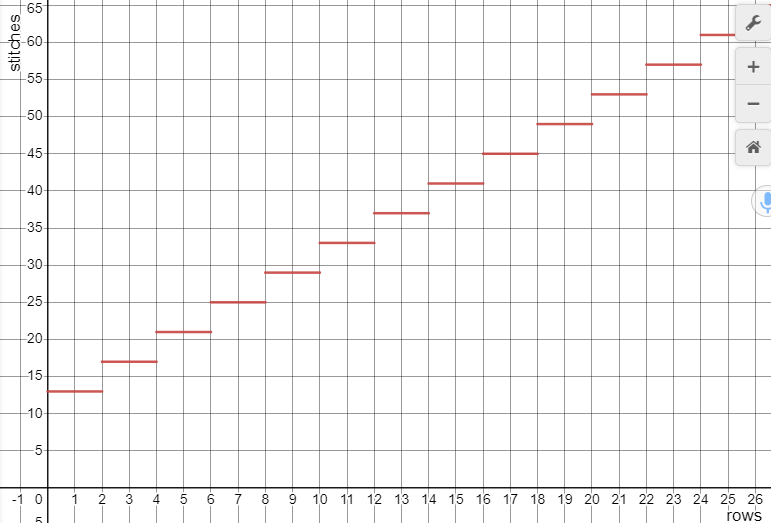
Below is a graph of stitches I need to make to create any given row. So for example in Row 16 and Row 17, I have to make 45 stitches.

So to find the total number of stitches from row 1 to row n, I have to take the integral of this function.

So to find the total number of stitches in the entire shawl, I’ll take the integral from 0 to 168.

And two things become apparent. First, we get the answer we expected from the calculations in the previous post: 30,072 stitches. Second, we have a Riemann Sum that looks like a bunch of mini-rectangles, but since we’re doing so many rectangles, it almost looks like we’re taking the integral of a line and estimating it using a Riemann Sum!

So what line is this?

The line is y=2x+11. Why? Every 2 rows of stitching should increase by 4 stitches. So each row we move up should increase 2 stitches. And the +11 comes from the fact that the first row has 13 stitches! So 2(1)+11=13.

Let’s check a little more to ensure we’re thinking properly! The number of stitches forrow1+row2=13+13=26. And when we take the integral of 2x+11 from 0 to 2 gives us an area of 26. (We can intuit that visually from the graph or algebraically by calculating the integral.) And similarly, the number of stitches for row3+row4=17+17=34. And when we take the integral of 2x+11 from 2 to 4 gives us an area of 34.

So let’s say g(x)=2x+11 is a function that gives the number of stitches in row x.

So if we want the total number of stitches from row 0 to row n, which we’ll call T(n), we have to integrate this function:

Whaaaa? Oh right! That’s precisely the equation we got in the previous post by the arithmetic sum! It’s the cumulative sum of stitches, not how many stitches per row.

And so let’s see how many stitches are needed in the first triangular section, second triangular section, third triangular section, etc…

Oooh this matches (as we’d expect) what we saw from the previous post:

Lastly, I was curious when I’d be halfway done with the Shawl. Since there were 30,072 stitches in the shawl, I wanted to see what row would give me the halfway stitch. It is row 117.245. Since each triangular section takes 12 rows to knit, that would be when I’m knitting the 9th triangular section of the shawl!

I was also thinking we could answer this using a basic geometric idea. When we finish the first triangular section, it has area A. Then when we finish the second triangular section, it has area 4A. Why? Because the second triangle is similar to the original triangle but with all sides twice as large. Thus, the area increases as the square! When we finish the third triangular section, it has area 9A. And so forth! So after the 14th triangular section, we have an area of 196A.

So the total area of the whole shawl is 196A. So half the area would have an area of 196A/2=98A.

This would happen after we finish the 9th triangular section (an area of 81A) and the 10th triangular section (an area of 100A). Yay, our geometric understanding matches our algebraic understanding!

Fin. (For now.)