This is going to be a writeup for a math problem I’ve been working on for a professional development thing I’m doing this summer. The question related to soap bubbles. Because I just want to get something up, for now I’m going to quickly say that the problem I’ve been tackling reduces to this:

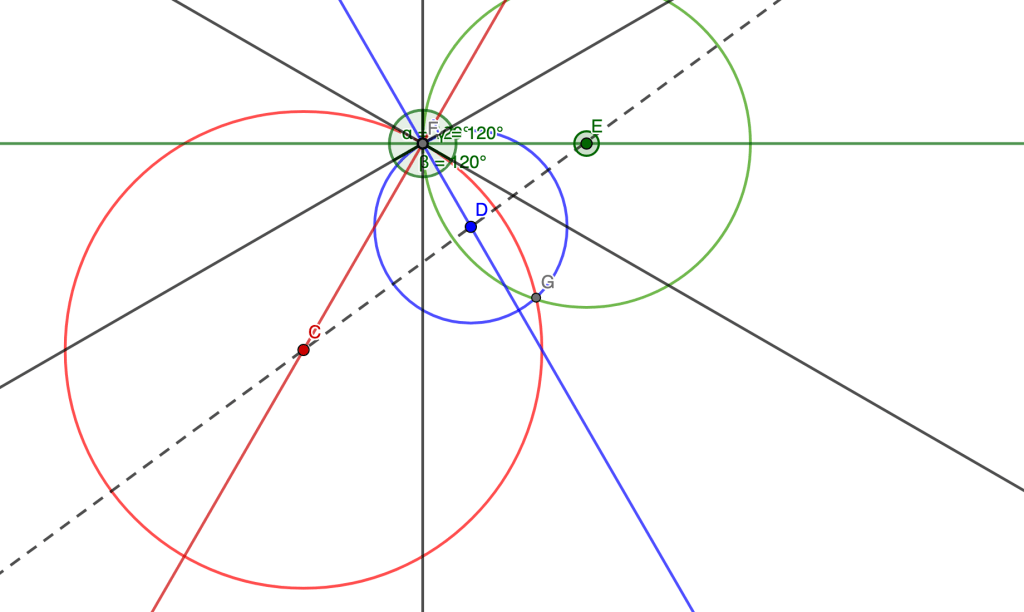
Let’s say I have two circles that “intersect at 120 degrees” like in this diagram below (if you zoom in enough at to the intersection point of the circles, the two circular lines are approximated by the tangent lines I drew, and the tangent lines form 120 degrees to each other):

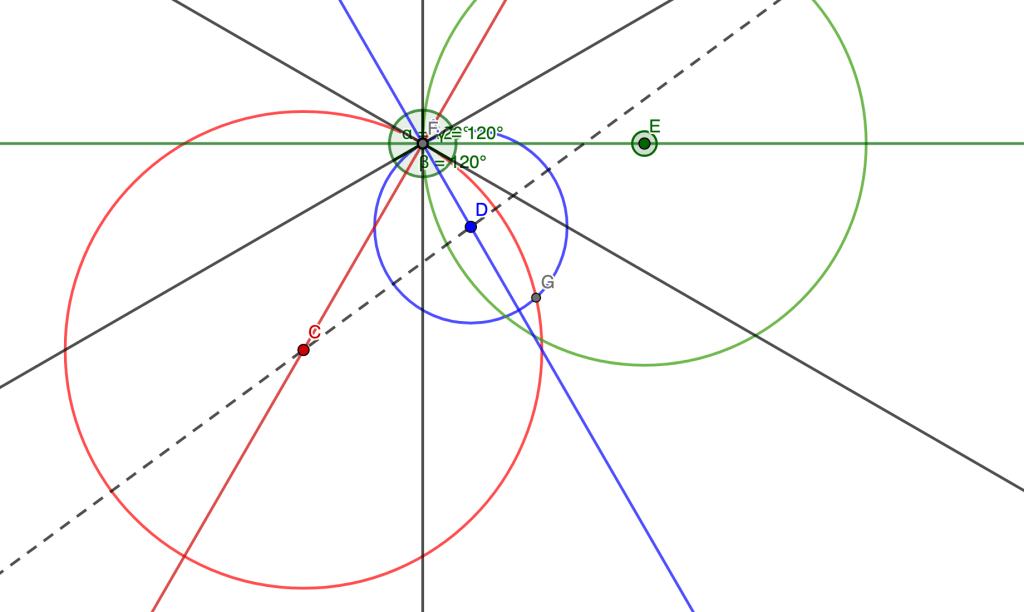
It turns out that there is a THIRD circle which can also intersect with these two circles and form 120 degree angles. Here are some different configurations that showcase this.

The question I’ve been dealing with is this: given the two initial circle radii (the red circle and blue circle, in the pictures above), can I come up with a formula for the radius of the third (green) circle?

Here is the applet I made to play around with these circles [https://www.geogebra.org/classic/kaynpexw].

I’ve been working for a few days to find the answer. I felt at times I was going in circles (no pun intended), and indeed I was. When I got the answer, I was astounded.

It was much more elegant than I anticipated! Everything simplified in a beautiful way. And my work was so ugly… I mean, I was using the Law of Sines and the Law of Cosines and the sum of angles formula for sine… so after taking a break from the problem, I went back to see if I could do it much more simply, now that I had played around with the problem and better understood the contours of it. I could!

First, I had to show that the angle formed by the radii to the intersection point had to be 60 degrees.

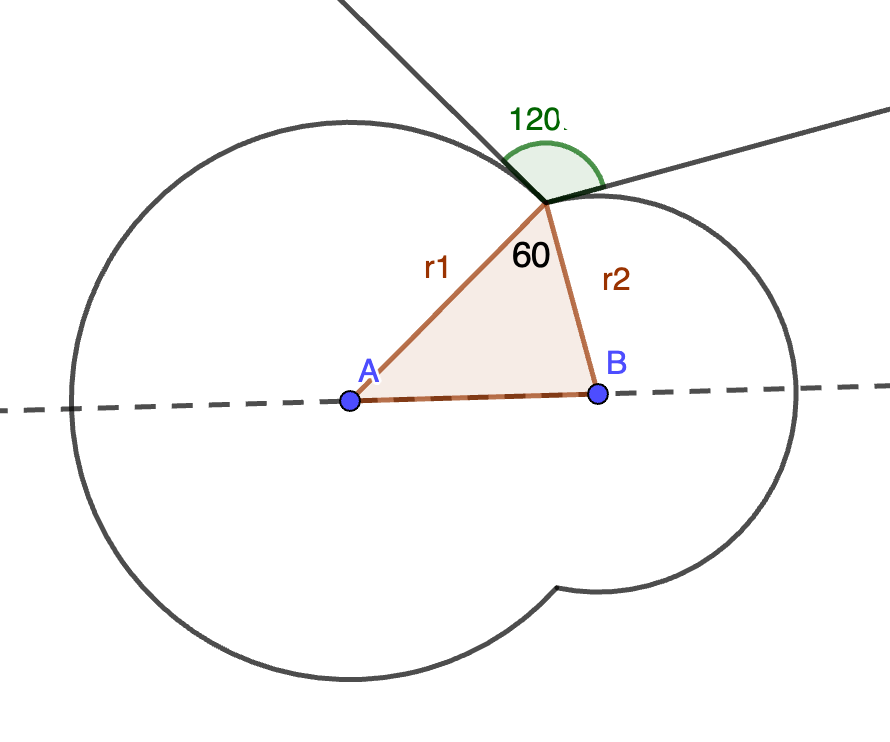
Here’s my work for that, using the fact that the tangent lines to the circles form right angles with the radii.

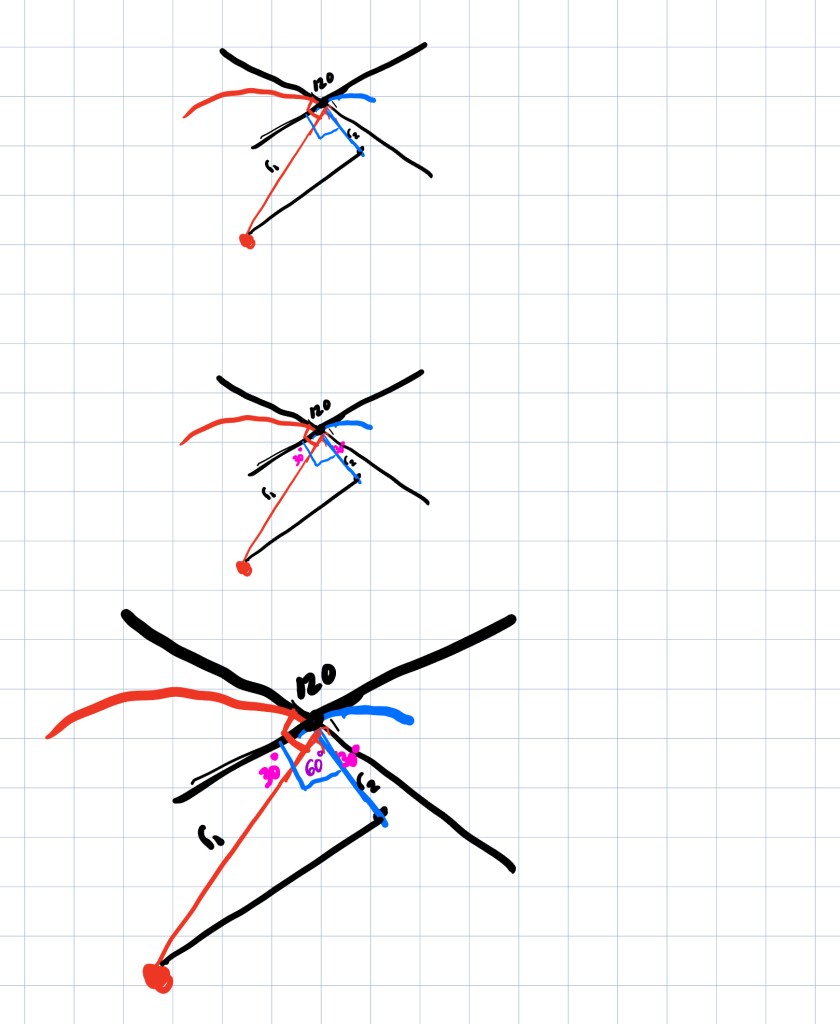
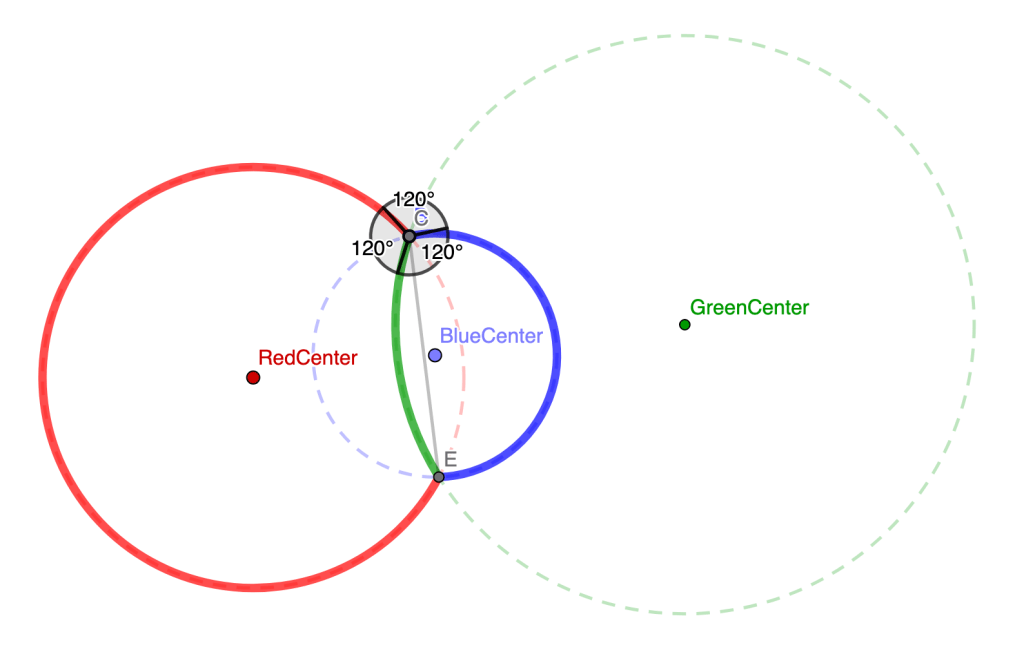
I next added in the third circle into the picture. Here’s a very not-pretty applet I made [https://www.geogebra.org/classic/wysfbqwn]. Drag point E and see what happens… I’m getting all possible green circles that intersect the red and blue circles at 120 degrees. There are an infinite number of them!

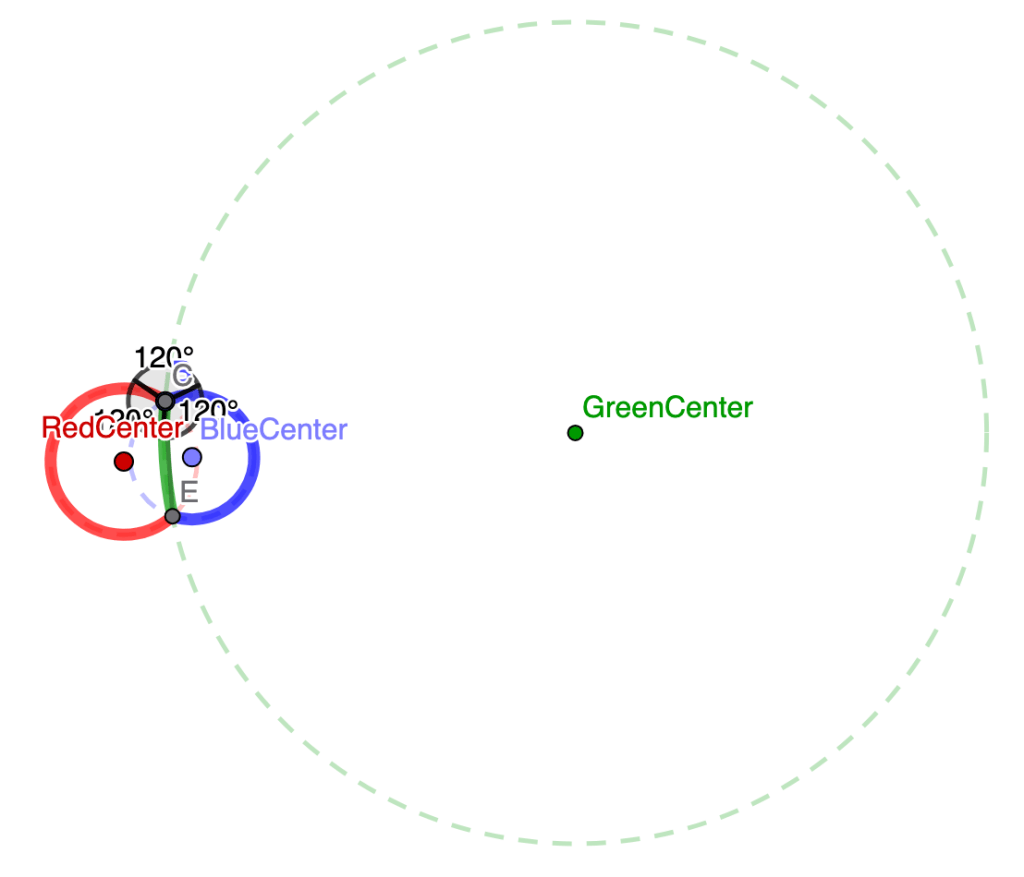
If you just want to see the picture, click through the images below to see what happens as I change the radius of the green circle to gradually bigger and bigger and bigger.

There are an infinite number of green circles that work! However, only one of the green circles also intersects at point G, the other location where the red and blue circles also intersect. So that’s the green circle we want. It took me a hot second to reason out why point E has the lie on the same line as C and D. I’m just trying to get this posted, so I’ll add that reasoning in later if I have time.

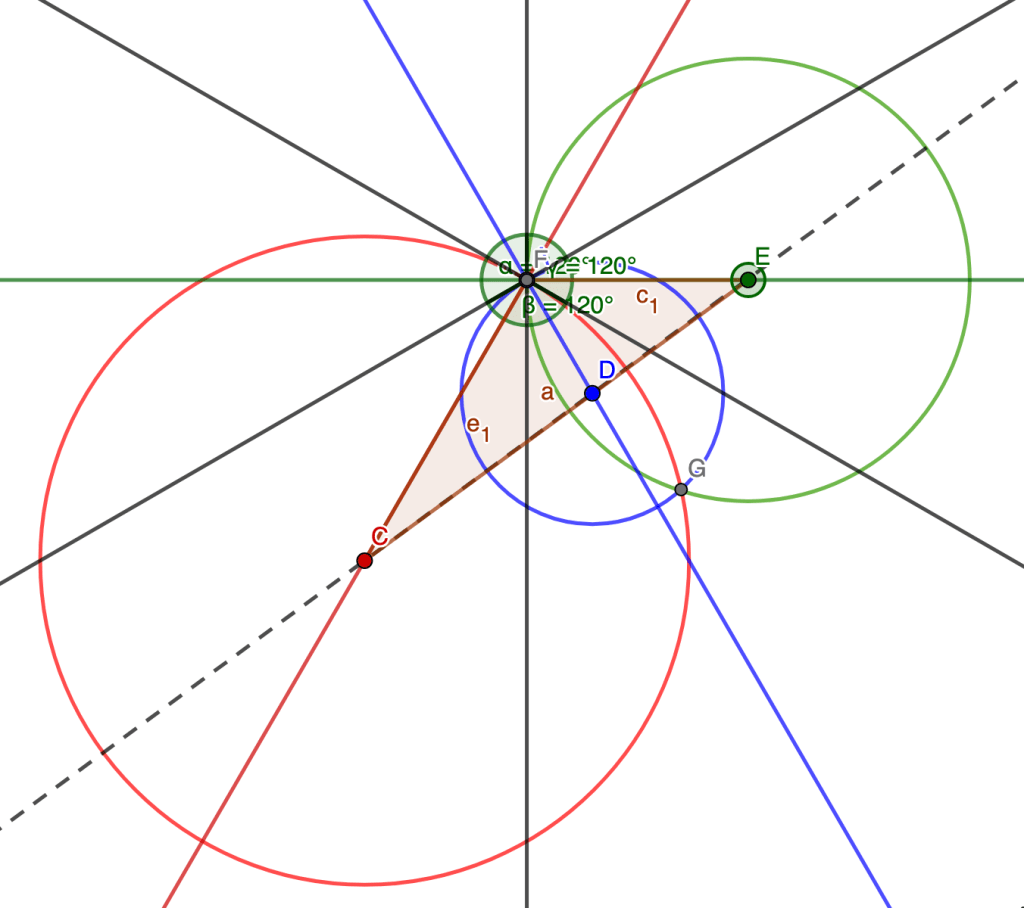
At this point, for me, the problem involves focusing on the triangle highlighted below:

I’m going to look just at the triangle now. We showed that the angle between r1 and r2 is 60 degrees. An identical argument can be used to show that the angle between r2 and r3 is also 60 degrees.

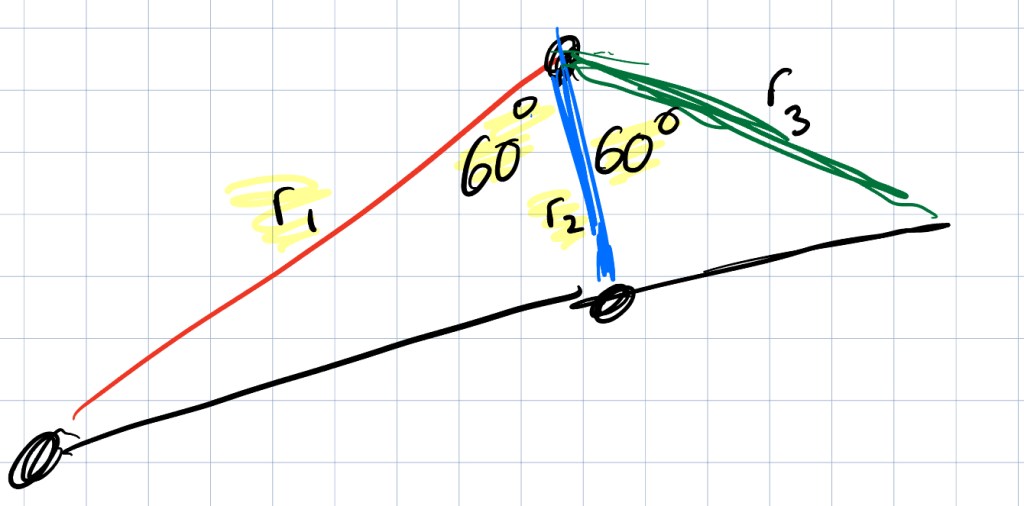
To keep things straight in my head, I highlighted the things we know in yellow. We are given r1 and r2, and we know the two angles are 60 degrees. We just have to find r3, which is the radius of the third green circle!

At this point, I think there are lots of things one can do. In my original work, I was using lots of Law of Sines and Law of Cosines. But in my revised work, I didn’t need any of those things. I decided to rotate the triangle.

And the reason I did this is to put everything on a coordinate grid. From here on out, my work just fell out nicely! On the diagram below, I found the equation of the purple line. And then I wrote the equation of the line that forms r3 (what I’ll call the green line). And then I found the intersection point of the purple and green lines (the green point). And then I found the distance from the origin to the green point.

And that formula below is precisely what I found in my messy, convoluted first attempt that took hours and wasn’t as elegant.

Writing this formula in reciprocal form, we get either the first or second formula:

I remember from when I taught multivariable calculus that the measure of curvature of a circle is the reciprocal of the radius. So in that formulation, the curvature of the third circle is the difference in curvature of the other two circles.

Beautiful!