Calculus

You know it’s a bad sign…

You know you’re a bit rusty from the summer when a teacher asks you to — without using L’Hopital — to prove that:

$\lim_{x \rightarrow \infty} \frac{\ln(2x)}{\ln(3x)}=1$

And you are like, oh, that’s easy.

And then — after two false starts — it takes you 3 minutes to figure out.

Just remember: you are a calculus teacher.

I’m going to say it again: you are a calculus teacher.

Maybe if I say it enough times, it will be true.

(more…)

Mid-Day Calculus Question

I asked a question to the two AP calculus teachers today, and I think we’ve concluded that we each aren’t 100% sure of the answer. It’s one of those questions that seems so basic that how could we not be sure?

I’m going to put up two graphs (of the square root of x). Can you tell me what intervals the following function are increasing on? [Notice the difference: Function A is defined at x=0, Function B is not defined at x=0.]

FUNCTION A

FUNCTION B

According to Anton’s Calculus text, it says:

Let $f$ be a function that is continuous on a closed interval $\text{[}a,b\text{]}$ and differentiable on the open interval $(a,b)$ .

If $f'(x)>0$ for every value of $x$ in $(a,b)$ , then $f$ is increasing on $\text{[}a,b\text{]}$ .
If $f'(x)<0$ for every value of $x$ in $(a,b)$ , then $f$ is decreasing on $\text{[}a,b\text{]}$ .

According to Rogawski’s Calculus text, it says:

Let $f$ be a differentiable function on the open interval $(a,b)$ .

If $f'(x)>0$ for $x \in (a,b)$ , then $f$ is increasing on $(a,b)$
If $f'(x)<0$ for $x \in (a,b)$ , then $f$ is decreasing on $(a,b)$

So my questions are: Are these two different definitions? I’m not teaching AP Calculus, but would this even be an issue for the AP exam? And why am I so not getting this?

Integration as Accumulation

I was downloading something yesterday and noticed that my downloading program tells me the download speed, and it updates it every half second or so. It also tells me how much of the file I’ve downloaded, total (e.g. 29.6 MB out of 64 MB, 46.3% completed).

This is a perfect example of integration as accumulation! The integral gives you the total amount of the file the program has downloaded. The graph above — created by a bittorrent program called $\mu$ -torrent — creates a graph of the download speed over time. [1]

This actually would be a great way to have students come up with the conceptual idea of Riemann sums themselves: given a thousand data points, collected every half-second, of the download speed, what would be a good way to figure out how much has been downloaded. How would you estimate it?

And you could extend it to say: if you wanted a quicker but less accurate way to come up with how much has been downloaded, how would you do that? Students might say, “take every fifth data point” or “average every five data points” or come up with some other interesting method!

Or you could ask if there is a more accurate way to come up with how much has been downloaded. And there’s a good chance, with some requisite prompting and asking the right questions, that they could come up with the Trapezoidal Rule. And then you could segue into Simpson’s Rule.

Note: I know, I know, you could do the same thing with a speed v. time graph (giving you distance), or any other number of graphs. But I like this. It comes naturally out of things we do everyday!

[1] I cribbed this from here.

Calculus Projects! Or, How to Combat Senioritis.

The year is coming to a close and I’ve found something to entertain my seniors. They’re taking regular calculus. More than likely, most of them will never take a math class again. If they are going to take math in college, chances are they’re going to be taking calculus over again (I don’t teach the AP calculus classes at my school).

My school treats seniors with the deference that seniors think they deserve. They don’t have to take final exams, they don’t go to classes after May 22nd (don’t ask), and they miss a lot of May to AP exams. All in all, because of these restrictions, May is pretty hard to plan, if you teach a senior class.

I gave my last quiz recently, and I’m having students use their class time to work on a calculus project.

I only have 7 students in this class, so I decided to do something pretty radical. I pretty much gave them free reign on their project. I told them they could do anything they wanted — just as long as they’re passionate about it. They have to do something they’re going to enjoy doing. They could also choose the point value of the project (a large quiz grade or test grade).

At this point, the only way I’m going to get them to do anything is by tapping into things they like.

So I had them brainstorm, we met individually so I could guide them, and they’re off to the races, with some great projects:

One student is doing a study of Newton’s method (we didn’t cover it in class) to find the zeros of a polynomial. She’s going to compare whether Newton’s method to finding zeros is “better” than a more simplistic method of finding zeros. That method, in case you were wondering, has you find an interval where you know there is a zero (e.g. for example, say you know there’s a zero on [-1,1] because the function is negative when x=-1 and positive when x=1). Then you divide the interval in half (into [-1,0] and [0,1]) and you find which of those two intervals has the zero. Then you divide that interval in half, and find which of those two intervals has the zero. On and on and on…
Another student is doing a study of rainbows, which involves calculus. (Awesome resources here and here.)
Another student really liked learning the intuitive version of the chain rule that I taught (post one and two), and wanted to make a lesson for my students next year on that! So she’s making a video tutorial and worksheet to accompany it.
In the same spirit of teaching, one of my students wanted to do something similar by making a video tutorial on the formal definition of the derivative.
One student is taking AP Physics B, but throughout the course, has noted connections between what he’s learned in his non-calculus-based physics class and what we’re doing in calculus class. One connection he made was between Pressure, Volume, and Work. He (rightfully) noted that $W=\int P dv$ . So he’s going to be making a presentation on this relationship by doing a bit of research and bringing application to the class.
Another one wanted to learn something “new” so I suggested he do some research on a hanging string. More notably, if you hold up a string (like a necklace), it will hang down due to gravity. Surprisingly (or not?) the shape is not a parabola. It turns out that it’s this funky shape called a catenary. He’s investigating why that’s the case, and how to derive the formula.
Last but not least, one of my students had difficulty with the sections on surface area and volume, because she couldn’t visualize the regions/spaces being formed. So she’s making two mechanical thingamajiggers out of wire. You bend the wire to be whatever function you’re going to be rotating, and then there’s a handle that rotates the wire. I am so excited about this one — I hope it works out so I can use the model next year in class!

Calculus and Chaos Theory

On the same blog, God Plays Dice, I learned two important things today:

(1) The Napkin Ring Problem, which basically says if you take a sphere, and cut out a cylinder from the center (and take off the two caps at the top and the bottom of the sphere), the volume of the remaining solid will not depend on the radius of the sphere at all!

In totally unrelated news, today we wrapped up our initial foray into finding volumes by slicing, by revolution, and by washers in calculus. I wonder what I’ll be doing with them tomorrow. I dearly wish I had an interesting problem for them to work through. Sigh.

(2) Edward Lorenz is dead.

All those years ago (okay, not so long ago) I was at MIT getting my first taste of chaos theory. I took this course with Daniel Rothman, who is an amazing teacher, and who taught from an amazing textbook (Strogatz). I loved the class so much that when I was asked if I was interesting in grading the problem sets for the following year’s class, I jumped at the chance.

It was in that course that I was first introduced to Edward Lorenz and his paper on weather (!) which launched a whole phenomena: chaos. But I also got so into the subject that I tried to fix a broken chaotic waterwheel that was being left unused in the basement of MIT. (I was unsuccessful, though I still wrote my final paper for a class on a modification of the Lorenz equations.) And when I was in graduate school, I was asked to write a “history of chaos theory” article for an encyclopedia that never really got published (to my knowledge). Also when I was in graduate school, I traveled to Beijing for a summer school (4 weeks) on complexity and chaos, thinking that I might want to do my dissertation around the topic of complexity and chaos in the sciences. And now that I’m teaching in high school, I wanted to introduce some of the budding mathematicians to the topic, so in math club, I gave a 3 part mini-lecture on chaos and the logistic equation.

Needless to say, chaos = cool. When I took that initial class with Prof. Rothman, Lorenz came to give a guest lecture. I’m sad that he’s gone. He is partially responsible for a really interesting part of my life that keeps recurring, no matter where I am or what I’m doing.

If you want to read my encyclopedia entry on the history of chaos theory (which is okay, but I’m sure has a number of problems with it), I’ll post it below. It talks about Lorenz’s contribution, if you don’t know.

(more…)

Birthday Polynomials

A few days ago, JD2718 wrote a post about “Birthday Triangles” — having students create three coordinates out of their birthdate and then analyzing the triangle that these coordinates make.

Even though it’s just a bit of fun, and you could have students work with any sets of points you give them, there is something great to be said for students creating their own problems that they feel ownership of. As JD2718 writes:

Best evidence, (and mind this, please) almost every class, when they first plot their own birthday triangle, there is one or two sad looking kiddies (it’s not come to tears, but I’ve seen the quivering lip) who thinks their own triangle is ugly. “Nooo” I say “Yours is obtuuuse. Does anyone else have an obtuse triangle that looks as nice as Anna’s?” (it’s usually a girl)

I thought that this idea could work in calculus too, creating “Birthday Polynomials.” My first thought was exactly JD2718’s: take the three birthday coordinates and find a quadratic that would fit them. But that would be a precalc assignment. (With bonus question: With what birthdays could you not create a quadratic?)

But I wanted more. I wanted to come up with something awesome. Something calculus. Something that would knock my students’ socks off. I initially thought something like this… if I was born on April 21, 1978, the birthday polynomial could look like: $f(x)=4x^3+21x^2+19x+78$ [1].And questions could be: where are the local maxima and minima? where is it concave up and concave down? where is it increasing and decreasing? And of course you could do things with integration too…

But there’s something unsatisfying about that type of question. It’s nice, but I want to wow! my students. I want to knock their socks off. Show them something elegant and unexpected. So I thought…

I want them to create a polynomial using their birthdate which would have an inflection point that was their age.

I was planning on using this amazing property [if there’s a cubic equation that hits the x-axis three times, then there’s a point of inflection, and it will be the average of these three x-intercepts] they would have to discover.

So if my birthday were January 25, 1980 (it is not), and we evaluated this polynomial on March 30, 1980 (after I celebrated my birthday), a birthday polynomial might look like this:

$f(x)=(x+1980*3)(x-2008*3)(x)+1x+25$ .

$f(x)=(x+year born*3)(x-2008*3)(x)+month born*x + date born$

[Note that the month and date play no role when finding the point of inflection… they are red herrings.]

But there are many annoying problems with this… First of all, that 3 is annoying. Second of all, that 2008 gives some of the fun away. I guess multiplying it by 3 and writing it like 6024 would help disguise it, but not much. Third of all, if I worked the problem on January 5th (or anytime in the year before January 25th), it would get my age wrong by a year. Fourth of all, it’s not elegant.

I’ve spent a little time tweeking it, and thinking of ways to rework it… but I haven’t anything elegant or clever yet. For now, it’s going to have to go on the backburner. Spring break is over and school is starting tomorrow and I have too much on my plate.

I’ll post an actual, good, interesting way to come up with a birthday polynomial with some amazing property (that somehow magically spews out your age, perhaps) when I have time…

[1] Of course I had to do a google search on “birthday polynomial” to make sure I wasn’t reinventing the wheel. One calculus teacher in Texas did something similar.

How knowledge becomes tacit, or how my calculus students rail against u-substitution

Recently in calculus, we’ve been working hard on u-substitution to solve integrals. Integrals are not intuitive. They are motivated (area under the curve), they are justified (the anti-derivative), and we try to play around with them until we “get them.” But when it comes down to it, you can’t really capitalize on much intuition when introducing them.

In my class, the most we did with honing intuition was to ask basic questions like these: 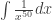$\int 5dx$ , $\int x dx$ , $\int x^3 dx$ , $\int x^\frac{1}{2}dx$ , $\int \frac{1}{x^{50}}dx$ , and $\int \sin(x) dx$ .

To solve them, students had to “work backwards” from their derivative knowledge. They were just guessing and checking to see what functions they could take the derivative of to get, say, $x^\frac{1}{2}$ . (In this case, it was $\frac{2}{3}x^\frac{3}{2}+C$ ). They figured out some general strategies on their own, and I validated them.

And then we moved on to u-substituion, to solve integrals like $\int (2x-9)^5dx$ and $\int \frac{10x}{\sqrt{1-4x^4}}$ .The hardest part of u-substitution is picking a good u which actually simplifies the integral. (In the first integral, $u=2x-9$ and in the second integral above, $u=2x^2$ .) The question for students is: why? It would be a mistake to assume that any explanation you give them will make sense (initially). For the second integral, saying–

“Well, because I see that square root on the bottom, I immediately think of inverse sin, because we know $\frac{d}{dx} \sin^{-1}(x)=\frac{1}{\sqrt{1-x^2}}$ . Hence, I see that we should pick a u which makes the integral take this form, and hopefully replacing dx with something in terms of du will cancel out the numerator.”

–will never work. You can say it until you’re blue in the face, but until they try out a whole bunch of possible us which get them nowhere, until they’ve seen enough similar questions like this, until they try to articulate for each integral why they chose that particular u, then they won’t gain intuition. You can’t force it. It comes through familiarity.

This is one of those topics where I think new math teachers probably dread introducing (and if they aren’t concerned about it, they are better people than I am). Students invariably will be confused. And what’s worse (from the student perspective) is that there isn’t a procedure or routine to get the answer. It involves guessing (a u). Educated guessing, but guessing none the less.

A few students have been freaking out — they just don’t “get it.” But I promise them that if they keep at it, it will work out. But they need patience, practice, and to reflect on each step of what they’re doing (why am I picking this particular u?). I’ve designed my lesson plans around these three elements: we’re going slowly, we’re doing tons of problems, and students need to be able to articulate some reason why they chose a specific u. I want them to know that this is a process they need to go through to come out better on the other side.

As Math Stories eloquently puts it:

Learning is not easy. If it was, we wouldn’t need schools and teachers. My kids frequently say that something I’ve taught them is easy. That’s once they’ve learned to do it – it’s the reward at the end of the process. While they’re learning it, they whine and complain and get headaches and have to use the bathroom and everything else imaginable. But that knowledge can only be integrated into their heads by experience, by wrestling with the fundamentals, by trying it out and repeating it and seeing how it works together with other things they know. They may eventually learn shortcuts that make things easier for them, leaving the methods they cut their teeth on in the dust. There are many teachers who will jump straight to the easiest methods, because that’s how the students will end up having to apply it in the real world. But jumping ahead, providing easy technological solutions for things they would otherwise struggle with, is just robbing them of an opportunity to really really learn.

Except for that one unnecessary word (“technological”), this quotation is exactly how I feel now. I will probably show it to my kids too.

Continuous Everywhere but Differentiable Nowhere

I have no idea why I picked this blog name, but there's no turning back now