Calculus

Related Rates: See ’em in action!

A short while ago, I attended the Teaching Contemporary Mathematics conference at the North Carolina School of Science and Mathematics (NCSSM). Before leaving for the conference, I had just started related rates with my kids in calculus. I have had a problem with related rates — because the problems are so bad. It’s just one of those places where you feel: this is where calculus should come alive.

But it doesn’t.

Well, at the conference, one of the last lectures I attended was given by Maria Hernandez. The lecture was ostensibly on using video in the precalculus and calculus curriculum. But in actuality, it was a solution to my related rates problem. Maria had created a wonderful, short activity which brings to life — visually — the idea of related rates.

I stole it, slightly modified it, and used it in my classroom the day after I got back. The activity’s best quality is that students could see math in action, not only from the use of the video, but also from the graphs they produced from analyzing the video. We’d been spending months on this “take the derivative” “take the derivative” “take the derivative” that I felt like we were losing all the understanding we had built up for abstraction. It was perfect to bring us back to basics. I enjoyed doing this in the classroom, and so I asked her if I could share it here. She generously replied:

Of course you can write about the video projects on your blog and feel free to share the worksheets. You can add my e-mail address so folks can send me a note if they have questions.

Maria’s email is: hernandez at ncssm dot edu

Things to note:

1. All my kids have school issued laptops with Logger Pro installed. (I’ve also heard very good things about the free program Tracker which does the same things as Logger Pro.)
2. All my kids used Logger Pro in other classes, and although most weren’t experts at it, it wasn’t completely new to them either
3. This is all Maria Hernandez’s work… I am just sharing it and my experience with it in my classroom. But if you love it, send her an email shout out!

Prelude

You teach the basics of related rates, in the same, boring way you always do. Blow up a balloon, and ask what sorts of things are changing as the balloon blows up. (Volume, surface area, circumference if you assume it’s a sphere, tension in the rubber, etc.). Then you start talking about how these things are all connected — if you have a bigger volume, you have a bigger surface area — and as one changes, the other changes too. And related rates are how these things are changing in relation to each other.

Go through some basic problems together. I use this packet of problems — where we do some together as a class, some they work with a partner, and some they do on their own. In general, I don’t do the harder related rates problems, because for my (non AP) class, I care more about them getting the fundamental ideas.

The Video

Now it’s time to show the kids The Video.

[Maria has put the video up for you to download here.]

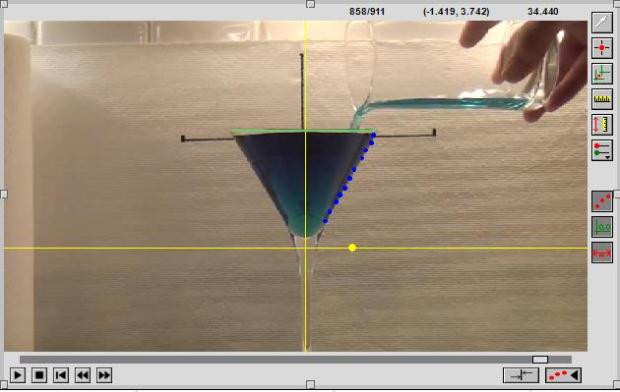
Play them the video once, then ask them to jot down things that are changing in time while you play it again. They will come up with things like radius of the cone, the volume of the cone, the height of the cone, the surface area of the cone, the amount of water that is being poured out of the beaker, the angle of the beaker, etc.

The Question

Here’s the question you should pose: “The person who tried to pour the water into the glass tried really really really really hard to pour it at a constant rate. Watch the video again. Do you think he did a good job?”

So play the video again, and then when they’re done, pose another question:

“How does the rate of change of the volume of water being poured from the beaker relate to the rate of change of the volume of the cone?”

[Note: I’m glad I anticipated this. Interestingly, it wasn’t totally obvious for my kids why the two rates of change would be the same.]

The Task

So then you let them know their task. They’re going to be using related rates to check to see if the person pouring the water did a good job pouring it at a constant rate. To do this, they’re going to use (a) a guided worksheet and (b) Logger Pro.

Set them off on the guided worksheet. Maria’s original guided worksheet (with Logger Pro instructions!) is here. My (very slightly modified) worksheet is here:

View this document on Scribd

Let them at it however you want. In one class, I had them work on Section A and then we had a discussion about their results. In another, I let them move onto Section B without discussing their results until the end. You can figure out what will be best for you.

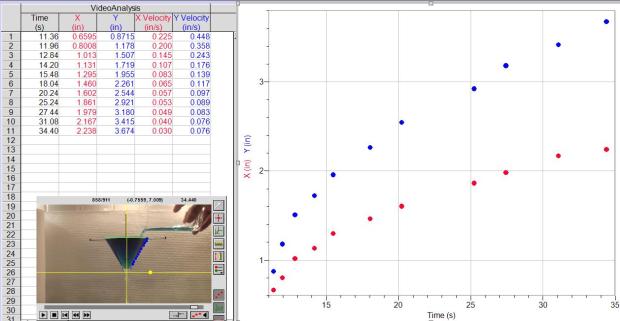
The general idea behind the worksheet is that students make predictions, and then use Logger Pro to evaluate their predictions. First, students capture data using Logger Pro…

The yellow lines are our coordinate axes (the origin being at the “bottom” of the cone). The dots give us something special. As we play the movie, frame by frame, we add these dots at various times showing where the water is at these times. Notice the wonderful thing about recording the dots on the edge of the class… the x-coordinate of these dots represents the radius of the cone, and the y-coordinate represents the height of the cone.

Once the movie has been marked up with blue dots, students can see what wonderful things Logger Pro gives them!

Not only does Logger Pro make a graph of radius v. time and height v. time (lovely!), but it also gives us a spreadsheet set of data… at each time that we made a dot, we are given the radius, the height, and for free thanks to Logger Pro, $\frac{dr}{dt}$ and $\frac{dh}{dt}$ .

Awesome! Well using the fact that $V=\frac{\pi}{3} r^2 h$ , we can conclude that:
$\frac{dV}{dt}=\frac{\pi}{3}(2r\frac{dr}{dt}h+\frac{dh}{dt}r^2)$ .

Oh, how nice. Logger Pro gives us all our unknowns in that spreadsheet so we can calculate $\frac{dV}{dt}$ . And isn’t that what we cared to find out? If $\frac{dV}{dt}$ was changing at a constant rate?

Some things of note:

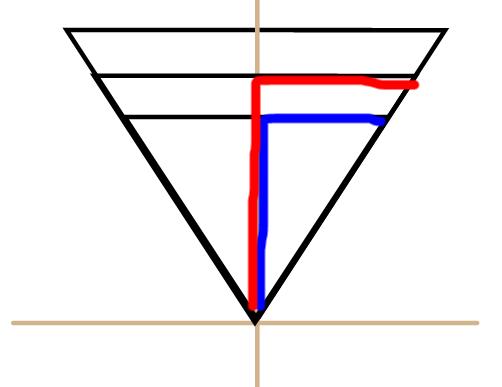
1. When discussing Section A, you can have a very nice discussion about your students’ predictions. It was cool to discuss why the general shape of r vs. t and h vs. t should be very close to each other. In fact, if you draw the cone filled in at different heights, you can use similar triangles to argue that however fast r is changing, h must be changing at a proportional rate. Why? Similar triangles!

2. In one class, I gave my kids class time to work on the Logger Pro part of the activity. In my other class, I had them work on Logger Pro at home. It was clear to me that the class who worked on Logger Pro in class enjoyed the activity more. There was more discussion, and they had people to talk to when they had technical difficulties. The class that had to do Logger Pro at home was not super pleased by it!

The Conclusion

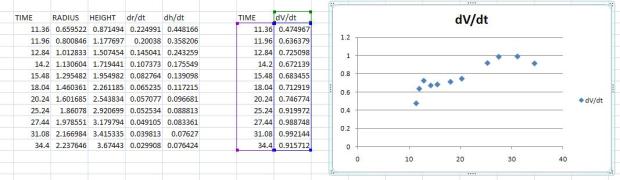
My kids used the guided worksheet to calculate $\frac{dV}{dt}$ at a bunch of different times, and to graph $\frac{dV}{dt}$ v. time. It turns out (we used Excel) we get something that looks like:

My kids all conclude that the person pouring the water doesn’t do a good job.

I’m not quite done yet, though. I ask them one last question… If the graph for $\frac{dV}{dt}$ v. time looked like:

“this would mean that the guy was pouring at a constant rate… because the data almost fits a line.”

I tricked almost all my kids in both of my classes, when I said it like that… But one kid in each class caught on that I was faking them out. And they said that this doesn’t mean the water was being poured at a constant rate… but that more and more water was being poured out over time. The only way we would be assured that the water was being poured out at a constant rate is if our data fit a horizontal line…

Nice.

Extensions

I’ve been thinking… perhaps in the fourth quarter I am going to have my students make their own videos filling up cylinders and cones. In a group of 3, I was thinking of asking them to make 2 videos:

trying to pour the water in at a constant rate
trying to pour the water in in such a way that the graph of $\frac{dV}{dt}$ v. time has a special shape I give them (a decreasing line? a bell curve-y shape?)

Basically it’s going to be a challenge for them, and I’ll have some sort of prize for the group that can get the water in at the most constant rate, and a prize for the group that can get the water to pour in the special shape I give them. Of course the bonus for me is that I might get some more videos to use in future years…

Where do I go from here?

Today in one of my two calculus classes today, we got on the topic of $0.\overline{9}$ .

I think it came up when we were talking about how to approximate the instantaneous rate of change in a problem: we had a function $v=20\sqrt{T}$ , and we wanted to estimate the instantaneous rate of change when $T=300$ .

So a student said let’s pick another point, such as $T=299.99$ . And we found an approximate instantaneous rate of change. Of course I asked “how could I get this answer more precise?” and someone said “add more 9s!”

So we realized we could pick a closer point, such as $T=299.9999999$ .

Of course, then we had some precocious youngster say: “why not get it super duper exact and plug in $T=299.\overline{9}$ ?”

Ah hah. Many of them thought that $299.\overline{9}$ was SUPER close to, but definitely not equal to, 300.

I went through the whole standard argument, which usually convinces most kids:

Let $x=299.\overline{9}$ . Then $10x=2999.\overline{9}$ .

So $10x-x=2700.$ Which means $9x=2700$ . Which means $x=300$ .

I thought I had them. One student said I was breaking her worldview.

Ha.

But then, THEN, they asked me an awesome question.

One said, and the others jeered: “Isn’t $299.\overline{9}$ kinda breaking the rules of what you’ve been saying. How infinity is a concept? How this decimal goes on forever? And you said we couldn’t mix concepts with numbers. We can’t write $6(\infty)$ or $\infty+6$ because we’re mixing concepts and numbers. So why can we talk about a number with a decimal that goes on FOREVER? Aren’t we mixing concepts and numbers? Isn’t this thing totally nonsensical?”

Okay, okay, they got me there. And they’re thinking deeply. And they’re getting me to think deeply.

So then I said: “okay, you have a point. So let’s see if we can mathematize this in a way that works with our understanding of things.” So I made a list:

$299.9=299+\frac{9}{10}$ .

$299.99=299+\frac{9}{10}+\frac{9}{100}$

$299.999=299+\frac{9}{10}+\frac{9}{100}+\frac{9}{1000}$

$299.\overline{9}=299+\sum_{N=1}^{\infty} \frac{9}{10^N}$

But then I noticed we are still mixing infinity (as a concept) with these numbers because we’re adding an infinite number of them… so then below it I wrote:

$299.\overline{9}=299+\mathop{\lim}\limits_{M \to \infty}\sum_{N=1}^{M} \frac{9}{10^N}$

Now we’ve written this decimal as what it truly is: a limit as the number of terms gets large without bound. And the limit has a definite value — the sum is getting closer and closer to 1, as close as we want to 1, infinitesimally close to 1, so we can conclude the limit of the sum is 1. So we can conclude that this sum is 300.

And then, sadly, I moved on.

The kids were interested in this conversation, and I think it could get at the heart of what we’re doing with limits (and then relating it to derivatives), and how infinity is a concept (for us) and not a number. But I don’t know what to do from here, where to go from here.

I didn’t convince everyone, and I don’t want to go too far afield with this unless someone out there can suggest a good idea. I mean, this idea of the limit, two things infinitesimally close together, is powerful [1]. So is there a way to extend this discussion meaningfully? Philosophically? Anyone have any good activities out there, any good worksheets out there, any good readings out there, any good videos out there? I’m not even sure what sort of end goal I have. Just something that acknowledges the weirdness of repeating decimals, relating them to limits, and the concept of infinity…

For context for the class, this is the non-AP calculus class, where my kids are at very different levels of understanding.

[1] From my historical understanding, both Leibniz and Newton (and their followers) were still plagued with the idea that you would be kinda-ish dividing by zero when calculating the derivative, because they didn’t have the concept of limits in their formulation of calculus. This division by zero was unsettling for a number of contemporaries. And it wasn’t until Cauchy came along with his limit concept that he was able to give derivatives a solid philosophical foundation to rest upon.

CalcDave you’re the best

CalcDave posted some awesome questions to ask calculus students — to get them think of the very large and the very small… and I made a worksheet out of it. For posterity, I wanted to save some of the responses.

The least probable (but still possible) event that you can think of

Going skydiving with the president
That I will drop out of high school the day before my graduation
When I call ‘stop!’ my watch reads 12:00pm and 0.0000000001 seconds
Mr. Shah becoming a rock star in a band called “Pain in my asymptote”
A monkey typing a Shakespeare play on a typewriter
The Boston Red Sox winning the American League East
All the people in the world dying at one time
Winning the lottery
Pauly D not having a date and Snookie beating Jwoww in a fight
The Situation never having STDs
A 7.8 (richter scale) earthquake in NYC

Largest number

Draw the ugliest and prettiest functions

I asked the last question about pretty/ugly functions, because I assumed that most kids would draw continuous everywhere and differentiable everywhere functions. And for the ugly ones, those would be violated. We’d have asymptotes, holes, and non-differentiable points. My assumption was realized. So we’re going to have a talk about the aesthetics of math, and coming up with mathematical descriptions for “beautiful functions.” I want them to think about continuity and differentiability, without knowing the terms explicitly.

Now it’s going to be great. Whenever we start talking about infinity or infinitely small, we’ll have some juicy stuff to dig into — stuff they’ve mulled over. Even today, I was talking about watching a video of someone diving and pausing it. And then going to the next frame — and infinitesimally small amount of time afterwards.

We also zoomed in on a point on a graph a huge number of times. An almost infinite amount of time.

And the thing on the screen turned to look closer and closer and closer and closer to a straight line. But it never became a perfect line. Every point on the screen, as you zoom in, gets infinitely close to lying on a straight line. But it won’t ever be a straight line.

So great conversations. We’ll expand them as we continue. Especially how every (continuous) curve is an infinite number of infinitely small line segments joined together.

Intermediate Value Theorem

I wish we could do “baby posts” that were formatted different. Little asides that don’t warrant full posts. Like this one.

Anyway, today, the AP Calculus BC teacher (and all around awesome person) asked me if I had any good ways to introduce the intermediate value theorem.

That’s the most boring theorem ever. Saying that if you have a continuous function $f(x)$ on $[a,b]$ , and $u$ is between $f(a)$ and $f(b)$ , then there exists a $c$ in $[a,b]$ such that $f(c)=u$ .

In other words, if you have a continuous curve that goes from point $(x_1,y_1)$ to $(x_2,y_2)$ , then at some point along the curve’s journey from the first point to the second point, it’s going to pass through every $y$ value between $y_1$ and $y_2$ .

If you still don’t see it, just draw two points on a coordinate plane and try to connect them with a continuous function. You’ll see it then.

Anyway, it’s boring. So she was right to ask for ideas. I searched and found none.

So I suggested a warm-up for the class — before they know anything about this theorem. I asked her to throw this up on the board:

INDIVIDUAL CHALLENGE: I am so wise. I have drawn a function $f(x)$ on $[1,5]$ , with $10$ between $f(1)$ and $f(5)$ , such that then there does not exist a $c$ on $[1,5]$ such that $f(c)=10$ . Are you as clever?

And then I wrapped up some Jolly Ranchers for her to give to the first student who could do it.

She said it went really well. And it took a few minutes (read that: minutes) before the first student got it. Perfect warm-up.

The reason I really liked this idea, and wanted to share it, is because: (a) kids were motivated by it, (b) kids were forced to grapple with complex mathematical language, (c) kids got to play around (by drawing different graphs — a puzzle-y thing), and (d) kids discovered the Intermediate Value Theorem on their own.

Let’s think about the last point. The first 5 or so graphs students would draw would not satisfy the challenge. And they’d see the problem: that the graphs they were drawing were continuous. So the only way to satisfy the challenge would be to make their function discontinuous. So not only would they learn the IVT, but they’d really remember the restriction: you need a continuous function for the IVT to hold.

I’m sure many of you probably introduce the IVT this way. It’s certainly not new or revolutionary. But I am now excited to when I get to teach the IVT.

PS. I also am really impressed by this consequence (click link to see proof). The consequence of total boringness happens not to be boring at all!:

The theorem implies that on any great circle around the world, the temperature, pressure, elevation, carbon dioxide concentration, or any other similar quantity which varies continuously, there will always exist two antipodal points that share the same value for that variable.

Two Worksheets

ONE

On Thursday, I’m going to be introducing absolute value inequalities. Last year I used the picture below as motivation.

I then tried to work backwards to show kids absolute value inequalities. It wasn’t too hot a success. Certainly the “application” wasn’t a motivator, and working backwards just confused things.

This year, I’ve decided to start with a warm up. Without them knowing anything, I’m going to ask them to do this for the first 7 minutes of class with their partners.

View this document on Scribd

I already can see the great questioning and discussion that this simple worksheet will generate between partners. And then, when we come together: WHAM! powerful! It’s a simple thing, but Oh! So! Delicious!

After that, after we see some patterns and make some conclusions… then, then I can throw up the picture of the bag, and talk about it meaningfully. And have kids work backwards from their own conclusions to finding a way to express that region mathematically, using absolute value inequalities.

TWO

I’m introducing limits tomorrow. I pretty much have carte blanche in what I do. Last year what I did was sad. Like SAD. Like: “Here’s what a limit is. Get it?” This year, I’m stealing pretty much from CalcDave wholesale. Here’s his calculus questionairre. And here’s what I made.

View this document on Scribd

Pretty much the same thing. Then I’d like to somehow have them start thinking about how to get velocity from a position versus time graph. Haven’t quite figured that out yet. Either that, or Zeno.

Putting it all together

On Friday I left home after the first two periods, sick. That’s not the bad news — I mean, we all get sick sometimes. The bad news is that I had already planned on leaving after the first two periods, to go to a wedding. I had to miss my friend’s wedding, to be sick at home. But I guess if there was a perfect time to be sick, it’s the day that I had already prepped sub plans.

I’m going to share ’em with you, because they worked really well.

The year is coming to a close, and I wanted my calculus classes to pause for a moment and take stock of what we’ve accomplished. I also wanted them to try to fit it all together in one large conceptual framework.

So I decided to ask ’em to — on giant yellow poster paper, with markers — create a concept map in groups of 3.

View this document on Scribd

I didn’t know what to expect. I hadn’t done this before. I did offer a prize to the best map (bag o’ candy).

I came to school on Monday, and was really impressed. The maps were colorful, comprehensive, and fun. I can only imagine the conversations that students had when drawing them (“remember when we did …”; “what was that thing we did with…”; “look at this!”).

A funny thing happened by accident. When I broke the kids into groups, I gave ’em group names (“The Polynomials,” “The Concavities,” “The Tangents,” and “The Anti-Derivatives”). There were just cutsie names, no thought behind ’em. I meant for each group to make a concept map for all of calculus. In fact, each group ended up making a concept map for their group name.

I’ll admit my initial reaction was disappointment, because they missed the “this is the entirety of calculus all together” aspect of what I was goin’ for. But then I looked at all four maps together — and they formed a pretty awesomely comprehensive map for the entire course.

Brainstorming Some Extensions/Changes

1. Use this as a 35 minute final exam review activity for a class — where each group takes a cluster of topics and connects them. Hang these up during review days for students to look at and refer to. (I might do this for Algebra II.)

2. If a course is broken into, say, 12 large conceptual units, ask groups to design one concept map for 4 random units they draw out of a hat — making connections among ’em. Then (somehow — this I haven’t figured out totally), have the class use these smaller concept maps to generate a giant map for the entire year.

3. Have students do this at the end of each unit, so they can visually see what they’ve learned and how everything relates to each other. (Possible studying technique for students who are detail oriented and can’t see the larger picture or how things relate.)

Their Homework

After this exercise, I gave my kids homework. I gave ’em a writing assignment, promising them I wouldn’t read ’em until after their final grades were entered. I do this for all my classes as they wind down.

For homework I’m going to ask each of you to write a letter from yourselves now to yourselves at the beginning of the year, telling yourself what you wish you had known about how to succeed in this particular Calculus class.

Something like:

Dear Sam from the Past,

Wow, what a long year. I can’t believe it is finally winding down. You might think it’s weird that I’m writing to you from the future, but I am. (The future is amazing.) Here are some important things to know so you can be successful in Calculus, and in life. Don’t wear Green. Mr. Shah hates Green. […]

You can talk about my quirks as a teacher (like “Mr. Shah does/doesn’t give a lot of partial credit” or “Mr. Shah doesn’t like when you use pen in class”), math things you wish you knew beforehand (like “you should make sure to really know your exponent rules” or “you should really be comfortable with fractions”), and any other general advice (like “trust me, doing your homework every day is key” or “Mr. Shah knows what he’s talking about so do everything he says without question” and “I found that cramming the night before did/didn’t work”).

You can and should also say whatever you want about the class — if you found it rewarding, if it’s really tough to visualize things, if meeting with me helps, if it’s impossible to do well, whatever. I won’t read them until after your final grades are calculated. Feel free to be funny — like if you look at yourself at the beginning of the year, and you hate that sweater you wore every day, warn yourself not to wear that sweater because it’s stupid. Or if you stole a teacher’s cupcakes, and you want to warn your previous self not to be so selfish, you can do that too. Don’t stress yourself out if you’re not funny.

I use these to create “Advice from Students Past” packets to give to my students next year (here too) — advice which might resonate with ’em on how to succeed. It also gives me some insight into my own teaching and my own class from my students’ perspectives.

So that was all from last Friday, a day I missed.

MEAN (grrr) value of a function!

In calculus today I was talking about how to find the average height of a function. Some kids just have a hard time understanding the concept. I always show them a few functions on certain intervals and I ask them what they think the average height would be. Just to initially test their intuition on the concept.

Some see it, and understand it; some don’t. All certainly have trouble articulating why they chose that value.

So I have two things that work for me, when explaining this. There’s some handwaving, but the focus is on the idea, and building intuition.

The first thing is we talk about how we would approximate the average temperature somewhere:

We take a bunch of temperature readings, and we add them together and divide by the number of readings.

How do you make it more accurate?

Continuous Everywhere but Differentiable Nowhere

I have no idea why I picked this blog name, but there's no turning back now

Calculus

Related Rates: See ’em in action!

Where do I go from here?

CalcDave you’re the best

Intermediate Value Theorem

Two Worksheets

Putting it all together

MEAN (grrr) value of a function!