This year, as I have been in the past few years, I’ve been attempting to incorporate more writing in my math classes [note: Shelli found a post from 2009 I wrote on this endeavor]. It’s been extraordinarily enlightening, because what this has done is show me two things: (1) kids don’t know how to explain their reasoning in clear ways, and (2) I’m usually extraordinarily wrong when I think my kids understand something, and the extent to which I am wrong makes me cringe.
(wow, been too busy to shave, have we Mr. Shah?)
For the first point, I don’t actually do much. I ask them to write, they write, I comment. And we discuss (more at the start of the year, but I always let this go and I forget to talk about it a lot). In Algebra II, they get one or two writing questions on every assessment. And each quarter they had problem sets where they had to write out their thought processes/solutions comprehensively and clearly. Even though I didn’t actually do anything systematic and formal in terms of teaching them to write (mainly I just had them write), I can say that I’ve seen a huge huge improvement in their explanatory skills from the beginning of the year. What I used to get just didn’t make sense, honestly. A random string of words that made sense in their heads, but not to anyone reading them. But now I get much more comprehensive explanations, which usually include words, diagrams, graphs, examples. They aren’t usually amazing, but they’re not ready to be amazing.
For the second point, I realized that the types of questions that we tend to ask (you know, those more routine questions that all textbooks ask) don’t always let me know if a student understands what they’re doing. It just lets me know they can do a procedure. So, for example, if I asked students to graph 
Before having students write, I actually believed that if I asked that question (“What does this solution mean?”), almost all the students would be able to answer it. (“Like, duh, of course they can!”) But since asking students to explain themselves, explain mathematics, I’ve uncovered the nasty underbelly to what students truly understand. The horror! The horror! But now that I recognize this seedy underworld of misconceptions or no-conceptions, I’ve finally been able to get beyond the despair that I originally had. Because now I know I have a place to work from.
The counterside to this point is that when kids do understand something, they kill it.
This simple question I made for my calculus students early in the year, and this student response, says it all. I have no concern about this kid understanding relative maxs and mins. No traditional question would have let me see how well this student knew what was up.
For me the obvious corollary is that: we need to start rethinking what our assessments ought to look like. If we want kids to truly understand concepts deeply, why don’t we actually make assessments that require students to demonstrate deep understanding of concepts? I am coming to the realization that the more we keep giving the same-old-same-old-assessments, the more we are reinforcing the message (implicitly) that we don’t reallyreally care to know about their thinking. We are telling our kids (implicitly) that we are content if they show their algebraic steps. But as I’ve noted, my big realization is that students performing those algebraic steps don’t necessarily mean that the student knows what they’re doing, or what the big picture is.
I don’t know have an example of what I think a truly ideal assessment might look like, but I do know it isn’t anything like I gave when I started off teaching five years ago (has it really been five years? why am I not better at this?), and I do know that each year I am slowly inching towards something better. Right now, my assessments are fairly traditional, but with each year, they are getting less so.
Sorry if I’ve posted something like this before. I have a feeling I have. But it’s what’s been going through my head recently, and I wanted to get it out there before I lost it.
[1] Another good illustration might be having students solve 
Continuous Everywhere but Differentiable Nowhere 
I always ask on the first day of Alg 2 class “What does the quadratic formula tell you about the graph of a parabola?”
I learn a lot every time.
This post is so good, Sam. I feel ripples of shame because I say I want my kids to write more and I say I hate the tests I give, yet I’m not really doing anything to change how I test. I work hard to bring more discovery-based learning to my kids (so I’m trying to be kind to self and not feel the tidal waves of shame), but boy you’re dead on about kids giving us the correct answer and not know squat what that answer means.
Ahhh, it’s like you read my mind when you added at the end about -3x < 6 ! I was thinking this while reading your post about procedural and algebraic regurgitation. And also I just learned last week a great way to teach this using the number line, so no more of this "rule" of switch the inequality sign when blah blah blah.
Thank you!! I'm going to be better next year by following your lead here.
Sam
I love the question you posed with the student response. I had a colleague in NJ who had a series of problems regarding a character she called ‘Careless Carl’. She would present Careless Carl’s work on a problem and the students had to identify if he got the problem correct (rarely) or where his mistake in his work was. I think that what you were asking was a bit higher level but it feels similar to me. I have a new colleague coming in here in PA next year who will be teaching Calculus for the first time and I will be sharing with her many of the ideas I have been picking up from you and others in the blogging community. Regarding the last inequality. This might just be a hangup of mine, but I always write my inequalities from left to right and refer back to the number line for them. So, I switched the old rule of changing the inequality sign to a more universal change the order of everything I write rule. By referring to the negative sign as more of a negating sign I think that I have been able to help some kids see this rule as a bit more meaningful. Does that sentence make sense, or is it a random string of words that just makes sense to me…?
Hi Jim,
Thanks for your thoughts. If your colleague doesn’t have material and it is a nonAP class, I’m always happy to share my materials (some good, some bad).
With regards to your random string of words (hahaha), I don’t actually get what you’re saying: “I always write my inequalities from left to right and refer back to the number line for them. So, I switched the old rule of changing the inequality sign to a more universal change the order of everything I write rule.” I think you’re saying that if you have
you always rewrite it as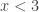 
, and I FORBID THE USE OF MULTIPLICATION OR DIVISION, how would we get the solution. Some come up with a graphing way (test points on a number line), but many actually finally (after some thinking) decide to add x to both sides and subtract 2 from both sides, to end up with 
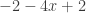, instead of using that whole “trick,” all they should do is rearrange the inequality so that the x does not have a negative coefficient… so 
. Then they can go from there.
That may be what you were talking about… but I’m not sure…
Sam
Actually, what I do when we first re-encounter the dividing by a negative rule I play kind of dumb and talk about how I am always bothered by negative coefficients. We take a few extra steps early on and add or subtract appropriately until my variable has a positive leading coefficient. I would always write 3 < x rather than x < 3 and this leads to some interesting discussions about how we read statements and what the number line tells us. In my first statement (3 < x) I tell them to look at the fact that x is to the right of 3 so the solutions correspond to numbers to the right of 3 on the number line. Conversely, if I write x < 3 then I note that the variable is to the left of 3 and the corresponding solution set is the numbers on the number line to the left of 3. They naturally tire of the manipulations and remember that the negative multiplier simply changes the order of the inequality statement. I don't know if this is any more lasting than remembering to switch the sign, but for some reason(s) it feels like a better explanation to me to tie in the order of the number line when discussing this. Thanks for pushing me into what I hope is a more coherent statement. I had been awake for less than 30 minutes as of my last post to you.
Also – thanks for offering to share. As we get closer to August I'll get in touch.
This is a great post and is something that I think about a lot too. I started having students journal every week or two, usually in response to a math problem with a bit more meat on it. They definitely improve their writing as the year goes on, but my main issue is that they HATE it and complain endlessly about how much they despise writing in a math class. Any tips on how to get past their resistance?
Hi Anna!
Yeah, my kids hate it, but they learned early on that I don’t want to hear whininess in our classroom [1]. Still, I don’t really care that they hate it. This is why. They hate it because it is not procedural. It is testing their understanding of a topic, and their ability to articulate that understanding. It’s putting together multiple skills. So it’s harder than just memorizing a procedure. And kids like to complain when something is hard. At the heart of it is the fact that they aren’t used to it.
Still, I’ve had ideas of not putting the writing questions on assessments, and giving kids a chance to incorporate feedback and submit a second draft, and things like that. Making a better feedback loop for them, and rewarding them if they improve. Maybe something like that could work, where they don’t see it as a threat, or as something that necessarily negatively affects their grades? Any ideas you give me would be appreciated on this too! I struggle with you.
Sam
[1] In fact, if a student starts whining to complain or ask me to do something, I tell them my ears just can’t hear when someone is whining. I tell them to take a breath, stop whining so I can pay attention to them, and ask me again. Of course I did it in a funny/jokey way. But doing that publicly worked wonders last year. This year I haven’t had as much a problem.
Thanks – I love the “tough love” approach. :) I think that you’re right about the reason for their resistance… many kids would really prefer to have a class where all they had to do was memorize and regurgitate algorithms, especially if that’s their perception of what math is supposed to be anyway. I do allow students to revise their journals for a higher grade, so I don’t think that they feel the writing assignments negatively impact their grades. It’s just that they involve more thinking and a higher cognitive load than a standard math assignment, and I have a small, but significant, number of students who just won’t do them and take the grade hit.
One idea I’ve been thinking about for next year is to incorporate smaller writing prompts into almost every daily assignment so that it’s even more a regular part of class and they get more used to doing it. Another thought is to have them do some of the journaling in class, which will at least ensure that all of them do it. It also helps if it’s something that other math teachers at the school are doing because then it becomes more of a “this is just what you do in math class” thing and not specific to my class.
Thanks for bringing this topic up. Happy to hear they’re are others that feel the way I do. Here’s something I tried this year that worked pretty well, and I’m thinking about incorporating it on a regular basis next year. It’s a five minute in-class assignment (but could be part of homework) and it involves writing a short paragraph.
“You have 60 seconds to explain ____________ to someone that knows as much math as you did last week. They must completely understand it after you explain it once. Go.”
It takes a little while for the students to understand it the first time you do it, but then it can become routine. It was a great assessment tool the couple of times I tried it. The students recognized how big of a challenge it was and kinda got into it. Furthermore, the students became self aware of their level of comprehension very quickly. It probably doesn’t lend itself well to more involved concepts, though.
I’m trying to think of a clever name that I can use once the students are familiar with the routine. No luck yet.
Have a good summer everyone!
This is a fascinating post and has really got me thinking. We have a coursework task in maths for our 17/18 year old here in the UK and they really struggle to write what they are doing. This has made me realise it’s because they don’t have any experience at it and has given me some ideas of what to do to prepare them the year before. Thanks.