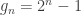Generating Fibonacci: Part II

We left off in our quest for an explicit formula for the nth Fibonacci number having created this amazing generating function: $g(x)=\frac{1}{1-x-x^2}$ .

To do what we’re about to do, I need to remind you of two precalculus things:

First, that $\frac{1}{1-pq}=1+(pq)+(pq)^2+(pq)^3...$ . If you don’t know why, I suggest doing long division!

Second, partial fractions.

I’m going to go through this explanation assuming you know these two things.

So let’s look at the denominator of our $g(x)$ and factor it. Okay, okay, you got me. There isn’t a nice factoring with integers. But it can still be factored, of course.

$g(x)=\frac{1}{(1-x\phi)(1-x\overline{\phi})}$ , where $\phi=\frac{1+\sqrt{5}}{2}$ and $\overline{\phi}=\frac{1-\sqrt{5}}{2}$ . Using partial fractions, we get:

$g(x)=\frac{a}{1-x\phi}+\frac{b}{1-x\overline{\phi}}=a(\frac{1}{1-x\phi})+b(\frac{1}{1-x\overline{\phi}})$

We’ve made good headway, but what we don’t know are $a$ and $b$ ! However, noticing that we can use the first precalculus topic above, that

$g(x)=a(1+x\phi+x^2\phi^2+...)+b(1+x\overline{\phi}+x^2\overline{\phi}^2+...)$ .

Rewriting this as a simple polynomial, we get:

$g(x)=(a+b)+(a\phi+b\overline{\phi})x+(a\phi^2+b\overline{\phi}^2)x^2+...$

Now we’re almost done! We use the initial conditions to find out $a$ and $b$ .

Since we know $F_0=1$ and $F_1=1$ , we can say $a+b=1$ and $a\phi+b\overline{\phi}=1$ . Solving these two equations simultaneously yields $a=\frac{1}{\sqrt{5}}$ and $b=-\frac{1}{\sqrt{5}}$ .

So the nth Fibonacci number is: $\frac{1}{\sqrt{5}}(\phi^n)-\frac{1}{\sqrt{5}}(\overline{\phi}^n)$

which simplifies to: $\frac{1}{\sqrt{5}}(\phi^n-\overline{\phi}^n)$ .

Which is what we set out to show! Huzzah! What’s also nice about this (besides the fact that it’s an integer, which is surprising) is that it shows that the Fibonacci sequence grows exponentially!

4 comments