Continuous Everywhere but Differentiable Nowhere

As you might know, this summer I’m prepping for the multivariable calculus course I’m teaching next year. When going through the textbook, I’m attempting some of the “challenging” problems near the end of the section. 

Today, when refreshing myself with the chain rule, I came across a problem which tested my intuition. And I’m afraid I’ve lost what little intuitive mojo I had years ago. I’m going to reproduce the problem below.

Question:

Suppose that the equation is expressed in the polar form by making the substitution and .

1. View and as functions of and and use implicit differentiation to show that:
   
   
2. View and as functions of and and use implicit differentiation to show that:
   
    
3. Use the results in parts (1) and (2) to show that:
   
    
4. Use the results in part (3) to show that:
    
5.  Use the result in part (4) to show that if satisfies Laplace’s equation
   
   then   satisfies the equation
   
   and conversley. The latter equation is called the polar form of Laplace’s equation. 

We know , so differentiating with respect to we get

(1)

We know , so differentiation with respect to we get

(2)

We now have a system of two equations, which we can solve for  and . Going through the motion yields the right answer.

How the heck in the n-dimensional universe did I miss this? I need to get on this, STAT!

I read the book a long time ago, but I remember it being about gender in the Victorian era. And math, of course. Am I totally wrong about this?

Today there was an Earthquake in Southern California. A NYT article said:

The quake, estimated at 5.4 magnitude (reduced from an initial estimate of 5.8), was centered 35 east of downtown Los Angeles in Chino Hills, just south of Pomona in San Bernardino county. It was felt as far east as Las Vegas and as far south as San Diego.

My first reaction, a question: how much of a difference was there in terms of the seismic energy released at the epicenter of the estimated earthquake versus the actual earthquake? How off was the esimate? I know that the Richter Scale is logarithmic, so the answer would be:

The estimate was over 2.5 times off.

But I realized: I know very little about the Richter Scale and how earthquakes are actually measured. How could an initial estimate be so wrong? I’m going to use this post to explain what little I’ve pieced together from the internet.

Jump on below!

(more…)

I was downloading something yesterday and noticed that my downloading program tells me the download speed, and it updates it every half second or so. It also tells me how much of the file I’ve downloaded, total (e.g. 29.6 MB out of 64 MB, 46.3% completed). 

This is a perfect example of integration as accumulation! The integral gives you the total amount of the file the program has downloaded. The graph above — created by a bittorrent program called -torrent — creates a graph of the download speed over time. [1]

This actually would be a great way to have students come up with the conceptual idea of Riemann sums themselves: given a thousand data points, collected every half-second, of the download speed, what would be a good way to figure out how much has been downloaded. How would you estimate it? 

And you could extend it to say: if you wanted a quicker but less accurate way to come up with how much has been downloaded, how would you do that? Students might say, “take every fifth data point” or “average every five data points” or come up with some other interesting method!

Or you could ask if there is a more accurate way to come up with how much has been downloaded. And there’s a good chance, with some requisite prompting and asking the right questions, that they could come up with the Trapezoidal Rule. And then you could segue into Simpson’s Rule.

Note: I know, I know, you could do the same thing with a speed v. time graph (giving you distance), or any other number of graphs. But I like this. It comes naturally out of things we do everyday!

[1] I cribbed this from here.

My sister told me this physics problem, and I have no idea how to solve it. It goes like this. There are two identical balls, one lying a distance x from the edge of a frictionless table, and the other being held up in the air, a distance x from the edge of the table. (See diagram above.) They are connected by a massless rope. 

At time t=0, the ball hanging in the air is dropped. 

Do you see what’s going to happen? That ball will start to fall down and approach the table, while the ball sitting on the frictionless table will be pulled toward the edge. 

Two questions, both of which I can’t answer:

(1) Which will reach the vertical plane of the edge of the table first? (In other words, will the ball on the frictionless table fall off the table before the falling ball hits the side of the table? Or vice versa? See my diagram below to see what the estimated path of the falling ball will look like. It curves towards the table, but also the distance from the corner of the table to the falling ball will increase as more time passes.)

(2) What is the equation for the path of the falling ball? (Again, see diagram below.)

It seems I was scooped.

In my ongoing obsession with the law and math (see post I and post II here), I learned that for many years, all the supreme court justices shake hands before each meeting.

The “Conference handshake” has been a tradition since the days of Chief Justice Melville W. Fuller in the late 19th century. When the Justices assemble to go on the Bench each day and at the beginning of the private conferences at which they discuss decisions, each Justice shakes hands with each of the other eight. Chief Justice Fuller instituted the practice as a reminder that difference of opinion on the Court did not preclude overall harmony of purpose. (here)

It still goes on today. There are 9 justices. A natural question: how many handshakes?

The “handshake problem” is a common problem in math classes. It’s equivalent to the problem of calculating the number of diagonals of a polygon. (Each vertex is a person; each line — including the edges of the polygon itself — represents a handshake.) It’s equivalent to adding the numbers . 

I was thinking it would be a good hook for a class where this problem was presented. Better than:

Assume we have n people at a dinner party who all don’t know each other. They all introduce themselves to (yawn) each other… (yawn)… and shake hands. How many (yawn) handshakes are there?

In the same sense that that’s not a true-to-life problem, neither is the supreme court handshake problem. But it’s a hook.

Of course, I looked it up to see if anyone else had thought of it (likely) and guess what? As I said: I was scooped.

I was so enthralled with Judge Sand’s city of Yonkers case that I couldn’t help but do a little more research on him. And lo and behold, nary a page in from a google search, I found another case that deals with math!

The setup

Henry Barschall, working for the American Physical Society and the American Institute of Physics, investigated the cost of science journal subscriptions for libraries. Even then in 1986 (as we hear is still the case now), science journals were increasing their prices — for a variety of reasons. And science journals were on average more expensive than journals in other disciplines (e.g. in 1985, the average yearly subscription for a science journal was $328, while for philosophy, it was only $47 — here). 

The survey was done and ready to be published in Physics Today. Barschall outlined his methodology here. The intial results which were published in 1986 are below:

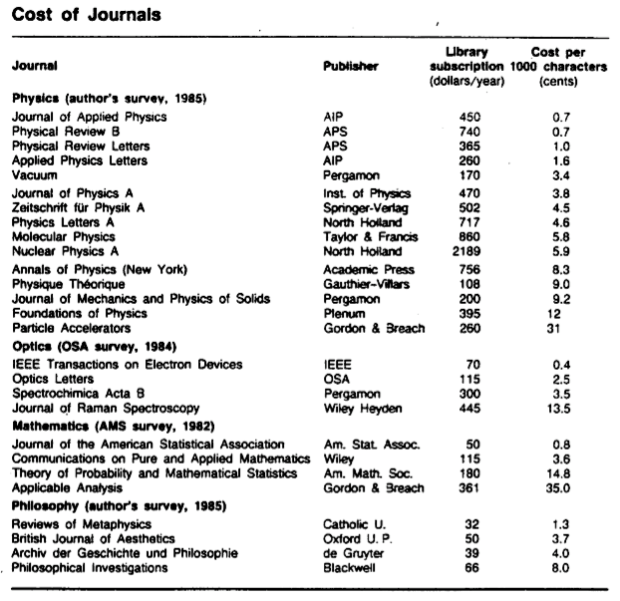
Note that for the physics journals, the American Physical Society and the American Institute of Physics were the most cost effective (0.7 cents/1000 characters), while Gordon and Breach were the least cost effective (31 cents/1000 characters). For this case, it’s important to note who sponsored the study! (The same organizations who came out the “winners.”)

An expanded survey, published in 1988, took into account not only the price, but the “impact” (or importance) of the journal… The metric for the impact was the average number of papers which cited an article in the journal two years after its publication. The more “impact” the journal had, according to the study, the more it mitigated a higher cost (hence: a ratio was created). 

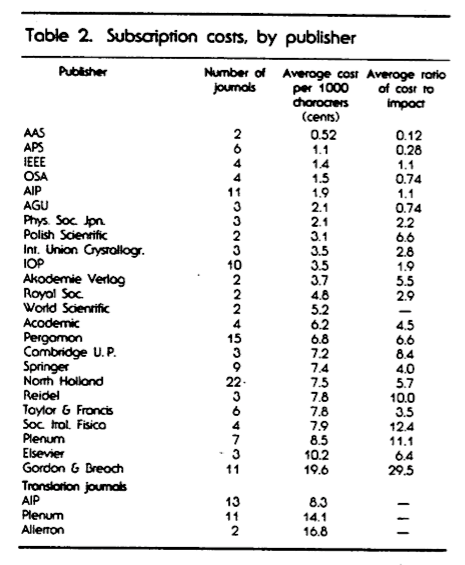
Again, APS and AIP were near the top of the list, while Gordon and Breach were way down at the bottom, with a cost/impact ratio more than twice the next publisher.

Gordon and Breach sued the APS and AIP. Judge Leonard Sand heard the case, and summarized it as follows:

This action, a dispute between publishers of scientific journals, raises an issue of first impression: whether a non-profit publisher may be sued for false advertising under the Lanham Act for publishing comparative surveys of scientific journals which, through the employment of a misleading rating system, rate its own publications as superior.

[...]

These articles, G&B alleges, constituted the start of a “continuous promotional campaign” waged by AIP and APS against them with the aid of Barschall’s survey results. First, G&B alleges, AIP and APS distributed “preprints” of the 1988 survey results to librarians (the primary purchasers of scientific journals) at a conference in June 1988. Since that time, G&B alleges, defendants have continued to disseminate the results of Barschall’s surveys to prospective purchasers through press releases, letters to the editor, “electronic mailings,” and meetings with librarians (“secondary uses” of the articles). G&B states that its attempts to reach an accommodation with defendants have been fruitless, and that it has been forced to resort to the courts. After filing a series of legal actions in Europe claiming unfair competition, and failing to receive satisfaction in Swiss, German, and French courts, G&B brought this lawsuit in September 1993.

G&B contends that the articles are promotional materials cloaked in the deceptive guise of “neutral” academic inquiry, and thus constitute misleading advertising under the Lanham Act, 15 U.S.C. § 1125(a), and comparable provisions of New York General Business Law. Barschall’s studies, G&B contends, far from being neutral, in fact constitute a “cynical promotional campaign” by AIP and APS to deceive librarians and other consumers of scientific journals into thinking that their journals have been “scientifically” proven to be of superior value. 

Judge Sand’s judicial opinions, the trial transcript (really interesting stuff! I swear!), Barchall’s papers, and other related material have been put on this site at Stanford for you to read. 

Eventually in 1997 (yes, justice takes a long time to render), Judge Sand made his final ruling:

Barschall’s methodology has been demonstrated to establish reliably precisely the proposition for which defendants cited it — that defendants’ physics journals, as measured by cost per character and by cost per character divided by impact factor, are substantially more cost-effective than those published by plaintiffs. Plaintiffs have proved only the unremarkable proposition that a librarian would be ill-advised to rely on Barschall’s study to the exclusion of all other considerations in making purchasing decisions. This consideration in no way makes Barschall’s study or defendants’ descriptions thereof false, and accordingly judgment is granted to defendants.

And the case is over!

Could this be useful in a math class?

I don’t know. I honestly can’t see myself using it next year, except maybe for a quick classroom discussion — a few “do nows” where each day I introduce more and more of the case and the evidence, and we talk about the math issues it raises…

1. Before presenting the data, it could lead to a discussion of how one might measure the cost-effectiveness of journals, and different ways students could imagine calculating them. 
2. Does Barschall’s method of measuring impact make sense? Does taking a ratio of cost per thousand characters to impact work? Why divide? (That will be hard for my students to get.)
3. A baby project: students could go to the school library and get data about various online databases that the library subscribes to, and try to determine whether subscribing is cost-effective for the school. Or at least, the class could try to brainstorm out what sorts of data we would want (e.g. the cost of the database annually, whether — and if so, how quickly — the cost of the database has been increasing, the number of times the databases are accessed each day, the amount of information the databases contain, etc.)

   But honestly, this seems like it isn’t really worth it. It would make for an interesting independent study, though.

4. A discussion about whether the survey was ethical or not, merely by virtue of the fact that those producing it were players in the game (non-profit players, but players none-the-less). [A similar discussion would be whether drug companies should produce their own studies of drug effectiveness.]
5. Ideas for how one might present the data visually? 
6. Should a court (even with scientific experts being called in) be the final arbiter in whether a mathematical study/survey was sound or not? If not, who should be? 

THE PROBLEM IS HERE!

In the Quach family, there is an age-old tradition that has been intact since the 1500s. In this tradition, every member of the Quach family receives one lottery ticket for his/her first 25 birthdays.

Based on empirical data collected over the years, it was determined by the family Mathematician that the probability of a Quach family member winning the lottery at least once during that 25 year stretch is 211/243.

Assuming the above statement is true, what is the probability of a Quach family member winning the lottery at least once during any 5 year interval? (Assume that lottery wins are completely independent of each other).

So the probability that a member of the Quach family does not win the lottery in 25 years is 32/243. Since winning each year is independent of any other year, we know:

P(not winning any year)=P(not winning 1st year)*P(not winning 2nd year)*…*P(not winning 25th year)

And since the probability of not winning each year is the same, we get:

P(not winning any year)=P(not winning in nth year)^25
32/243=P(not winning in nth year)^25
P(not winning in nth year)=(32/243)^(1/25) 

Now we need to find the probability of winning at least once in a five year interval, which is actually 1-P(not winning in 5 year interval).

P(not winning in 5 year interval)=P(not winning in 1st year)*P(not winning in 2nd year)*…*P(not winning in 5th year)

P(not winning in 5 year interval)=P(not winning in nth year)^5

P(not winning in 5 year interval)=(32/243)^(1/5)=2/3

Since we want to find P(winning at least once in 5 year interval), we know that that will have to be 1/3. 

I want me some of them odds.

I can’t help it… I have to post about this… jd2718 led me to a blog which is so awesomely captivating that I just spent the last hour reading like a zillion postings…

It’s not all flowers and sausages

It chronicles all the funny, frustrating, quotidian things teachers go through… you know what I’m talking about… there are those things which we go through and are funny to everyone

excerpt from blog: ”Well you need to get them to stop. We don’t need children standing there having orgasms. The next thing you know they will all be shivering and shaking and oooooohhhhhhhhh”

… and then there are those things that you only want to tell to other teachers because your friends wouldn’t get it

excerpt from blog: And as the cherry on my sundae, I ended my day with a doctor’s appointment. If that wasn’t sweet enough, I was correcting papers in the waiting room when my name was called. And she had the balls to say, “Oh look, you’re correcting papers, isn’t that cute!” I wonder if it would also be “cute” if Friday I run screaming from the building and bury myself face down in a cocktail?

Out of this list of 1001 books that one ought to read (from this book I guess), here are the ones I have read… about 5.1%. My favorites are marked with a *.

1. The Curious Incident of the Dog in the Night-Time – Mark Haddon
2. Middlesex – Jeffrey Eugenides
3. Choke – Chuck Palahniuk
4. Blonde – Joyce Carol Oates*
5. Memoirs of a Geisha – Arthur Golden
6. The Secret History – Donna Tartt*
7. The Hitchhiker’s Guide to the Galaxy – Douglas Adams
8. Them – Joyce Carol Oates*
9. In Watermelon Sugar – Richard Brautigan
10. The Crying of Lot 49 – Thomas Pynchon
11. The Bell Jar – Sylvia Plath
12. One Day in the Life of Ivan Denisovich – Aleksandr Isayevich Solzhenitsyn
13. Franny and Zooey – J.D. Salinger
14. To Kill a Mockingbird – Harper Lee
15. Pnin – Vladimir Nabokov*
16. Lolita – Vladimir Nabokov
17. Lord of the Flies – William Golding
18. Invisible Man – Ralph Ellison*
19. The Old Man and the Sea – Ernest Hemingway
20. The Catcher in the Rye – J.D. Salinger*
21. Nineteen Eighty-Four – George Orwell*
22. The Little Prince – Antoine de Saint-Exupéry
23. Their Eyes Were Watching God – Zora Neale Hurston
24. The Hobbit – J.R.R. Tolkien
25. Brave New World – Aldous Huxley*
26. A Farewell to Arms – Ernest Hemingway
27. The Sound and the Fury – William Faulkner
28. To The Lighthouse – Virginia Woolf
29. The Sun Also Rises – Ernest Hemingway
30. The Great Gatsby – F. Scott Fitzgerald
31. Siddhartha – Herman Hesse
32. A Portrait of the Artist as a Young Man – James Joyce
33. Ethan Frome – Edith Wharton
34. Heart of Darkness – Joseph Conrad
35. The Hound of the Baskervilles – Sir Arthur Conan Doyle
36. Jude the Obscure – Thomas Hardy*
37. The Adventures of Sherlock Holmes – Sir Arthur Conan Doyle
38. The Picture of Dorian Gray – Oscar Wilde
39. The Adventures of Huckleberry Finn – Mark Twain
40. Treasure Island – Robert Louis Stevenson
41. Alice’s Adventures in Wonderland – Lewis Carroll
42. Walden – Henry David Thoreau
43. The Scarlet Letter – Nathaniel Hawthorne*
44. Wuthering Heights – Emily Brontë
45. Jane Eyre – Charlotte Brontë*
46. The Purloined Letter – Edgar Allan Poe
47. The Pit and the Pendulum – Edgar Allan Poe
48. A Christmas Carol – Charles Dickens
49. The Fall of the House of Usher – Edgar Allan Poe
50. Pride and Prejudice – Jane Austen
51. A Modest Proposal – Jonathan Swift