So I encountered what I think is a horribly wonderful (and did I mention horrible?) problem. It took me forever to solve, because I kept getting different solutions and I didn’t know which was right and which was wrong and where my errors might have come from. But in the end, I think I finally got it right. The error was a silly sign error which made everything nice.
Here’s the problem [1]:
A length of sheet metal 27 inches wide is to be made into a water trough by bending up two sides as shown in the accompanying figure. Find and
so that the trapezoid shape cross section has a maximum area.
I don’t want to tell you what I got for the answer, in case you want to try it out for yourself, but I will tell you this: I was able to get a maximum area of square inches.
(And if you are banging your head against a wall, and need a solution for peace of mind, shout out in the comments. I’d be happy to type out my solution. I just don’t want to spend the time if no one cares.)
Update: I had posted as the answer, but again, I noticed a second silly sign error. I have never made so many algebraic errors on an problem as I did with this one.
[1] From Anton’s Calculus, 8th edition, Chapter 14, Section 8, Number 44

That was fun! I, too, get , with the maximum occurring when
, with the maximum occurring when 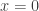 and
and  .
.
Ooops, that should be .
.
Cool! Wait, wow, LaTeX works in the comments? AWESOME!
What’s great is that for the maximum area we got, we can see that we can break up the trapezoid into three equilateral triangles (all sides of 9). Knowing that, I wonder if there’s a geometric way to show that the solution with maximum area would have to be this…
If you double the area, by putting a mirror image of the trough atop the original one, does the problem become one of maximizing the area bounded by a hexagon whose perimeter is 54?
And if you buy that, is it obvious that the solution is a regular hexagon?
And if that’s true, then if we turn this into a problem in 4 variables, with and
and  as given on the right, and a corresponding
as given on the right, and a corresponding  and
and  on the left, we still get the same optimal area.
on the left, we still get the same optimal area.
Or am I being daft? (Seems probable.)
I don’t think that a regular hexagon gives the largest area, actually. One of the weird things I remember learning is that there is a larger area hexagon…
http://mathworld.wolfram.com/BiggestLittlePolygon.html
http://mathworld.wolfram.com/GrahamsBiggestLittleHexagon.html
The hexagon talked about in the link about has a unit polygon diameter (the largest distance from one vertex to another). So couldn’t we scale the hexagon up until it’s perimeter is the one we want? The area of this hexagon will still be bigger than an n-gon with that same perimeter.
Which is super interesting, but it means that a regular hexagon doesn’t quite help us…
Or am I being daft? (Seems just as probable.)
Whoops, I take it back. Yes, the largest area of a n-gon with a fixed perimeter will be a regular hexagon. Blah.
Click to access onedollarproblem_mossinghoff.pdf
Interesting analysis of these types of questions. (I just skimmed it.)
I’d like to see your work. I know this is almost 3 years later now, but I can’t seem to get it to work. I got Volume to equal (27-2x)*(x*sin(theta)) + x^2*sin(theta)*cos(theta). Then I take dv/dx = sin(theta) * (27-4x+2x*cos(theta) = 0, which leads me to x= 27/ (4-2*cos(theta). Also dv/d(theta) = 27x*cos(theta) – 2x^2*cos(theta)+x^2cos(2*theta) = 0, which leads me to a bunch of gibberish which when I plug x into is even more convulted and i can’t solve it! haha, any help?.
Please show solution!!!