On Thursday, in Algebra 2, I aimed for understanding… and came up short. It was one of those lessons I went in excited to teach, because I knew I could get my kids to “get” it. And then, I didn’t. It wasn’t a bad lesson, and I don’t think my kids are the worse for it. But it just wasn’t that killer lesson I had hoped for.
The constraints:
I had 50 minutes to teach absolute value inequalities. I definitely had to get through “less than” absolute value inequalities (like , but I wanted to at least introduce “greater than” absolute value inequalities (like
).
The plan:
1. Start off lesson with a fundamental question raised by an image (found at 360).
2. Generate a basic understanding of what a “less than” absolute value inequality is, using a simple question to illustrate why there are many solutions. We would then fill in a number line from our solutions and then talk specifically about why our answer is not [-12,2], but actually (-13,3) (for the question below).
3. Point out the basic geometric interpretation, and tie that back to the initial question we wanted to answer.
4. Show how we can use this geometric interpretation, and a compound inequality, to help us come up with a method to solve these sorts of inequalities. (Work backwards.)
5. Formalize our method of solution.
6. Practice, practice, practice.
The outcome:
I only was able to cover “less than” absolute value inequalities, and I doubt that my students have a good understanding of why our solution method works. I do think my students will be able to follow the procedure though.
Where exactly did I fail? I failed in part 3 and part 4 of my plan. For part 3, I should have found a better way to explain the geometric meaning. My students didn’t “get” it totally. You can see part 4 of my plan executed here on my SMARTBoard slide:
As you can see, I tried to start from the compound inequalities and work our way to the absolute value inequality. At the end, there is this “ta da” moment which was actually more like “ta WHA?” They didn’t get what I was trying to show them.
And I don’t blame them.
A huge part of me doesn’t want to teach something without proving — or at least deriving by example — why something works. I feel like a fraud, like I’m teaching ’em magic instead of math, when I teach a method of solution first and then show where it comes from. But in this case, it would have gone over so much better if I had shown the method of solution, and then after practicing it a few times, took a moment to look at our work backwards to see why it worked. Talking about what each step means — algebraically and geometrically — backwards might have clarified things a bit.
I could have also designed the lesson in a totally different way. I could have worked off of our understanding of absolute value equations (e.g. the equation ). Then we could have had a great discussion on how to find solutions to
, focusing on why we use open dots at the solutions to the equality, and why we shade inbetween those dots. Now that I’m thinking about it, maybe I should remember to try this out next year.
If you want to see my entire SMARTBoard for the lesson, look below the jump.


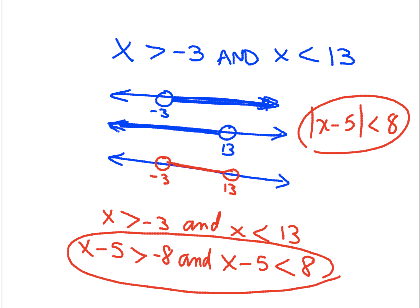
This year I went a little different route and did the functional analysis way. Abs(x) can be x or -x, so if abs(x) < 2, then (x) < 2 and -(x) < 2. It's probably less intuitive for them, but it's no less accurate mathematically, I guess. It also goes along with your, "Show me the steps, then tell my why later" thing. They seemed to do well with it, I think. Of course, they may have just learned the steps and then tuned out the rest.
Um. Genius. I don’t think it is less intuitive. I think it is MORE intuitive. Totally stealing this for next year. Thanks. Wow. Awesome.
If you happen to come back and see this…
How do you explain the “and” to them? (And that it is not an “or”?)
Ask them to try out both solutions
abs(x)<2
x-2 gives you (-2,2). Plugging in values verifies that this is the solution
x-2 is equivalent to (-infinity, infinity). This can’t be the solution.
for
abs(x)>2
x>2 and x2 or x<-2 which is equivalent to (-infinity,-2) U (2, infinity). Solution in those intervals work.
One other way is to expand on your distance examples. Show a picture of you and ask about the distances.
abs(x)5
Where are things more than 5 units away from you?
This treatment of absolute values as distances goes well with absolute values of complex numbers.
html is messing things up. not sure how I’d fix the comment.
I’m totally with you on the wanting to justify things before teaching them how to do it. My kids always yell at me “You always show us this complicated stuff and then wait to show us the easy way!”
I like the work amount of thought you’ve put into the lesson, it’s definitely better than anything I did with the topic and much more interesting. I taught this topic for my first two years, but after some back and forth in my brain I cut it out of my curriculum (I fortunately have the freedom to do such things). I feel its a topic that is difficult for kids to really understand, isn’t very much more useful than common sense in real life, and was never used in any of my higher math classes for anything. Correct me if I’m wrong on one of those accounts, but I’ve generally tried to cut out anything that has such a triple threat.
Anyway, the point is you’re not alone. This was always a difficult topic for my kids to really get, which is why my cost-benefit analysis has since removed it to make more time for more important topics.
Ha! That was my favorite comment from one of my calc students two years ago.
Okay, okay, I just had to look it up: “Mr. Shah likes to go the long way, the real building block method. First you learn the theory, then you learn the original (prehistoric) way, then (then!) you’ll learn the quick fun way. And later still you learn that you could have done it on your calculator all along! [Tutor] will want to teach you the quick way immediately and will moan and groan when you protest that Mr-Shah-hasn’t-taught-us-that-yet, but don’t give in to her wily ways! They won’t help you on the tests.”
As for cutting out of the curriculum or not, it’s a good question. Personally I would like to cut it out, because I don’t see much use for it. Except maybe for the definition of limits. But the chances they’ll remember it two years later, or even take away enough understanding that you won’t have to reteach it completely in calculus, is nearly zero.
definition of limits. But the chances they’ll remember it two years later, or even take away enough understanding that you won’t have to reteach it completely in calculus, is nearly zero.
http://en.wikipedia.org/wiki/%28%CE%B5,_%CE%B4%29-definition_of_limit
But on the other hand, it was only two days of class.
On Twitter, @jlanier suggested I teach it with “clouds”… so start with and talk about what that looks like (a "cloud"/shaded region of length 4 centered around 0). Then change it to
and talk about what that looks like (a "cloud"/shaded region of length 4 centered around 0). Then change it to 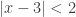 and how that changes the cloud. Then change it to
and how that changes the cloud. Then change it to  and how that changes the cloud.
and how that changes the cloud.
I really like that idea, but honestly, I think my kids would find all of this "magic"… I would lose them when trying to explain WHY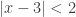 shifts the cloud 3 units to the right. Or why the cloud's length gets halved with
shifts the cloud 3 units to the right. Or why the cloud's length gets halved with  . I just don't think I could explain it well enough so they actually GOT it and didn't just accept it.
. I just don't think I could explain it well enough so they actually GOT it and didn't just accept it.
But that's probably my inability as a teacher, and not for the method of teaching it.
That transitions right into the transformation of functions that is so key in Alg2, though…translations, dilations, etc…might be a good place to introduce it as a “preview” to the function families unit…just a thought
I always teach abs. val. as distance from zero. So, for example abs(x-3) = 5 translates to “some number minus 3 will be 5 units away from zero” and then we solve and draw a number line to illustrate.
When it comes to abs. val. inequals, it’s still distance. For example, abs (x-3) 5 translates to “some number minus three will get us more than 5 units from zero.” We draw bunches of number lines for these problems to show each step.
Lastly, we talk about real life applications and draw number lines to figure out the abs val inequals.
-Amanda~
Ha! We were posting at the same time. It seems that you do what @jlanier does (see my reply to Mr. Sweeney).
Do you teach how to solve ? If you do, could you tell me how you explain that?
? If you do, could you tell me how you explain that?
Another way of saying |2x – 1| < 5 is that 2x is less than 1 away from 5. I find that easier to picture.
I teach the kids to read |2x – 3| < 2 as "The distance between 2x and 3 is less than 2" from which they figure out that 2x is between 3-2 and 3+2 and then that x is between (3-2)/2 and (3+2)/2.
They do then have a bit of trouble with |2x+3| < 2, realizing that they should read it as "the distance between 2x and -3", and similarly with |2x|, finding the 0 in there.
Still I think it's better than any purely algebraic approach, and it captures a lot more of the meaning of that kind of expression when it comes up in real life. Your example uses absolute value to talk about "distance", with |x-113|<3 or something like that.
For teachers/tutors in Singapore, it’s a major problem that students focus only on getting top grades, so instead of trying to understand they will resort to rote learning, and will just go through years of exercises from previous years, learning by heart the steps to get through different the types of questions they think will come up.
Short of having a teacher like yourself, who could really inspire children to like maths, what do you think they could do to learn? (I’m trying to get different opinions from math bloggers like yourself)