I’m going to post the way I worked out the two recent problems that I posted. Today I’m going to focus on the second problem first. Other people had different solutions they threw in the comments to the original posts, so you can look there too.
Statement: A particle is moving along the curve at a constant speed of
. When it reaches the point
, you know
. Find the value of
at that point.
Solution: I imagined the particle moving along the curve, and it being played on a film. The particle follows this path and is going at a constant speed:
So then I said: we only care about the particle around (2,2), so I mentally zoomed in near that point:
So we don’t care about the rest of the picture. The particle is actually moving in a straight line in the area we care about, and this line is (we found the equation of the line tangent to the original curve at the point (2,2)). So this greatly simplifies how I had to think about the problem. Where we care about things, the particle is moving in a straight line at a rate of
.
So then I thought about the velocity vector for the particle — moving in the direction of the line at a rate of . And this vector is composed of the velocity in the x-direction and the velocity in the y-direction:
and
.
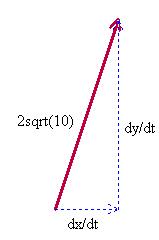 And we just have to use the last piece of information that we haven’t used… That the ratio of height/length of this triangle is 3 (the slope of the line — the direction of velocity — is 3). So we can solve this with a bunch of different ways, but I found the easiest to just make similar triangles and solve:
And we just have to use the last piece of information that we haven’t used… That the ratio of height/length of this triangle is 3 (the slope of the line — the direction of velocity — is 3). So we can solve this with a bunch of different ways, but I found the easiest to just make similar triangles and solve:
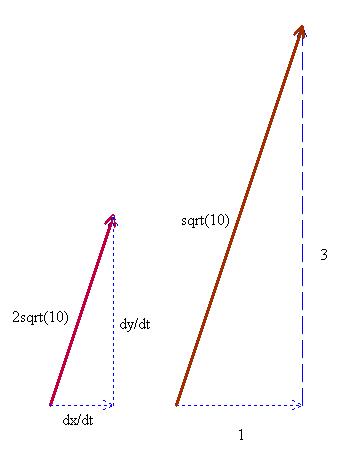 (I calculated that the hypotenuse of the second triangle was
(I calculated that the hypotenuse of the second triangle was .) Clearly we can deduce that
.
In essence, this is the exact same method that other people used to solve it, but it took me to actually zoom in and picture what was going on with the particle to figure this problem out so that I conceptually had mastered it.
The way I approached the second problem comes later.


PS. Don’t ask me why I made the second triangle bigger than the first one… I just wanted to show that they were different sizes. I just didn’t think “oh it would have made sense to make the larger triangle the bigger triangle.”
Man, Sam, you just explained that in a way that I think my 8th graders could understand it. Nicely done. I really wish that my calculus teachers would have made a problem like this seem so simple.