So a while ago, I mentioned to some of you on twitter that I was getting really frustrated with a particular problem we were presented with. I have a conjecture that I’m almost certain is true, but I can’t prove it.
Consider the unit circle . Plot
equally spaced points on the circle starting from
. Now draw the
chords from
to the others. What is the product of the lengths of all of these chords?
(There is an extension problem, which is changing the unit circle to an ellipse , for those who already have seen or find the original problem too easy.)
So feel free to write your own blog post with your solution, or throw your solution in the comments (just write SPOILER at the top so we know…).
What I’m interested in is if we could get a precalculus class to get the solution to this problem. Where they actually understand it. So if you had, say, 15 non-honors precalculus students and one week to work on this problem, how would you design the lesson?
I guess you have to have solved it or have seen a solution to know how to design the lesson. But even if you didn’t solve it (a la me!)… if there’s a solution you’ve read that someone posted in the comments… what would you do?
UPDATE: Mr. Ho has a great GeoGebra applet at his site; Mimi has some nice colorful diagrams and some explanation up at her site. Also, for those who want to wording for the ellipse problem… This extension I haven’t seen before, so I am citing Bowen Kerins (see comments below!) or Darryl Yong: “Take the diagram you drew in [the unit circle problem] and stretch it vertically so that the circle becomes the ellipse . All the points for the chords scale too. What is the product of the lengths of all of these chords?”
SPOILER (although just thoughts–not near paper or have time right now to work out actual details):
Seems like you could find the chord lengths by: 1. Create isosceles triangles for each chord by including the center of the circle. 2. Find the angle of the triangle that includes the center. 3. Since each triangle is isosceles, we know the other 2 angles. 4. Use law of sines.
SPOILER
I get the solution to be .
.
Proof: Since the points are all equally spaced around the unit circle, all the chords will be congruent to each other. So it suffices to find just the length of the chord connecting (1,0) with the first point encountered in a counterclockwise traversal of the unit circle, and then raise that length to the nth power.
Basic trigonometry tells us that the first of these encountered in a counterclockwise traversal of the unit circle (starting at (1,0)) will have x-coordinate equal to and y-coordinate
and y-coordinate  . (If you want to be fancy about it, these points on the circle are the nth roots of unity if you consider the circle to be in the complex plane.) Therefore, the 2D distance formula gives the length of the chord connecting this point and (1,0) to be:
. (If you want to be fancy about it, these points on the circle are the nth roots of unity if you consider the circle to be in the complex plane.) Therefore, the 2D distance formula gives the length of the chord connecting this point and (1,0) to be:
which simplifies to . Raising this to the nth power gives
. Raising this to the nth power gives
If that’s right (and I think it is) then you can get precalc students to work this problem (provided they have some trig) by getting them to think of appropriate simplifying steps. For example, realizing that all you need is ONE of the chords rather than all of them is a simplifying step, as is going for the simplest chord possible. Analyzing the problem with cases is good too — try n = 2 (so the answer is obvious, because there’s only one chord and it connects (1,0) and (-1,0)) and then n = 3… then they will get the picture, literally, and see you’re creating regular polygons.
The problem itself here isn’t so much the focal point as would be the problem-solving strategies students could dream up to solve it.
Well, drat, it seems I messed up about half my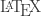 in that comment. Sam, feel free to fix it or jsut leave it, as you see fit. Sorry! I wish there were a preview button…
in that comment. Sam, feel free to fix it or jsut leave it, as you see fit. Sorry! I wish there were a preview button…
Done and done.
Unfortunately you’ve solved a different problem, Rob. The chords are all connected to (1,0), not from one to the next, so they should (generally) all have different lengths. Your method assumes all chords are the same length.
You’ve actually nearly given the form for the side length of an inscribed N-gon; use the double-angle formula for cosine (cos 2x = 2 cos^2x – 1) and you can get a version without a square root or a double angle.
1st time commenter – problems like this are why I loved math in high school. The intersection of geometry and algebra was/is very exciting to me.
If I were to teach this I think I might not jump straightaway to the question. This is a great opportunity for students to get to play with sequences and indexes, and really wrap their head around them. I would definitely have groups draw different circles for values of n, discuss possible values of each chord, of products of chords. Hopefully this would provide for a lot of entry points for students.
The analysis of different solutions could be valuable too. I didn’t actually use the distance formula, though many students would. Seems like a good time to discuss how we compare on solution to another/elegance.
At first I understood this problem differently from the 2nd commenter. Do all of the chords originate at (1,0)? Or do they go from 1st point to 2nd, 2nd to 3rd, etc. I went with the latter. (The former got me into product of a sequence formulas, which aren’t too familiar. )
SPOILER
I think I found a simple solution (which immediately raises suspicion that I jumped an assumption somewhere).
Like above, consider finding the length of the first chord, and raise to the nth power.
For the first chord, first consider the arc between the first two points. Its length is This is also the angle in radians between (1,0) and the 1st point.
This is also the angle in radians between (1,0) and the 1st point.
Consider the isosceles triangle formed by the radius to (1,0), radius to 1st point, and 1st chord. Bisect the angle between the radii, which will be perpendicular to the chord (chord properties). Now you have a right triangle with hypotenuse of 1 and an angle of . By trig the length of half the chord is
. By trig the length of half the chord is 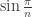 .
.

So the length of the whole chord is
Raising to the nth power yields
I tried a few test points (n=3,7,100) with the formula from the previous commenter, and it seemed to work out.
I have a clarification (in light of the solution above). The solution describes the products of lengths of a regular -gon inscribed inside of the circle. I feel like the problem you asked about has all the chords of connecting to the same point (so each chord is a different length, although there are probably usually pairs of chords of the same length). Just wanted to figure out what problem you were asking about.
-gon inscribed inside of the circle. I feel like the problem you asked about has all the chords of connecting to the same point (so each chord is a different length, although there are probably usually pairs of chords of the same length). Just wanted to figure out what problem you were asking about.
If the problem is as the solution described (which is how I first read it) you can also come to the same conclusion using the law of cosines, which is a nice exercise for having students utilize this identity (if they know it). In particular, it is nice because the students have to realize that the two lengths they know are of length 1 due to the fact that we are in the unit circle.
The problem asks for the the product of only the chords emanating from (1,0). Does that clear things up?
So if we are taking about n=4, we’re talking about the product of the lengths of the cords between:
(1,0) and (0,1)
(1,0) and (-1,0)
(1,0) and (0,-1)
That’s all. Does that clear things up?
It seems very complex to do this with anything but complex numbers. Suppose the angle of separation between the points is . Our points are then at
. Our points are then at  . Then the desired product is
. Then the desired product is
For equally spaced distributed evenly around the entire unit circle we have , for a final result of
, for a final result of
oops. I misinterpreted the problem. Never mind.
The answer for an -gon is most
-gon is most  , no? During my break between classes, I’ll see if I can write down a quick proof.
, no? During my break between classes, I’ll see if I can write down a quick proof.
Remove the word most from the first sentence.
What a nice problem!
SPOILER
I think there is a simpler answer. Let $\omega=e^{2\pi/n}$. Then the product of the lengths of the chords is
\[
P=\vert (1-\omega)(1-\omega^2)\ldots (1-\omega^{n-1})\vert.
\]
Now, let $Q$ be the polynomial
\[
Q=(z-1)(z-\omega)(z-\omega^2)\ldots (z-\omega^{n-1}).
\]
Note that $P=\vert\lim_{z\to 1}\frac{Q}{z-1}\vert. But on the other hand, the polynomial $Q$ has roots $1,\omega,\omega^2,\ldots,\omega^{n-1}$, so
$Q=z^n-1$. Hence
\[
P=\vert\lim{z\to 1}\frac{z^n-1}{z-1}\vert
=\vert\lim{z\to 1}nz^{n-1}\vert = n
\]
(L’Hopital’s rule!) So the product of the lengths of the chords is $n$. (You can check that this agrees with the previous solutions.)
This would be a good problem if you wanted to motivate spending some time learning complex numbers. Spend a day getting them to experiment with the problem, either with ruler and compass, or with something like Geogebra. Numerical experimentation leads to the answer $n$. But why? Let them keep thinking about the problem while you apparently go on to the unrelated topic of complex numbers (but get them to plot the solutions of $z^n-1$ themselves as early as possible…
I may have to steal this.
PS I’ve been following your site for a while now and have learned a ton. Thanks!
Nice proof, Andrew. I guess I won’t write down a proof between classes!
(Although, I suspect there should be a way to do this without involving limits or L’Hopital’s rule which would probably exclude it being presented to most precalculus classes.)
Ooops, I don’t seem to have a preview button. Let me try that again:
What a nice problem!
SPOILER
I think there is a simpler answer. Let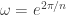 . Then the product of the lengths of the chords is
. Then the product of the lengths of the chords is
Now, let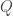 be the polynomial
be the polynomial
Note that . But on the other hand, the polynomial
. But on the other hand, the polynomial 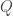 has roots
has roots  , so
, so
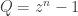 . Hence
. Hence
(L’Hopital’s rule!) So the product of the lengths of the chords is . (You can check that this agrees with the previous solutions.)
. (You can check that this agrees with the previous solutions.)
This would be a good problem if you wanted to motivate spending some time learning complex numbers. Spend a day getting them to experiment with the problem, either with ruler and compass, or with something like Geogebra. Numerical experimentation leads to the answer . But why? Let them keep thinking about the problem while you apparently go on to the unrelated topic of complex numbers (but get them to plot the solutions of
. But why? Let them keep thinking about the problem while you apparently go on to the unrelated topic of complex numbers (but get them to plot the solutions of  themselves as early as possible…
themselves as early as possible…
I may have to steal this.
PS I’ve been following your site for a while now and have learned a ton. Thanks!
That doesn’t seem to work. For example when n = 3, you have three points on the circle: (1,0) and . The length of one of the chords is
. The length of one of the chords is  . Therefore the product of the three chords is
. Therefore the product of the three chords is  , not 3. Am I missing something in the solution?
, not 3. Am I missing something in the solution?
Robert, you made the same interpretation mistake I did. Sam later clarified the chords are all relative to (1,0), not the product of the N equal length chords between each of the neighbouring pairs of points.
My calculus is rusty, but I am going to take a stab at how to break this down more simply (since you’re shooting for pre-calc level math anyway):
The kids should start by sketching and enumerating some concrete examples. I started with just the even n’s, and I got:
For n = 2, product of chords emanating from (1, 0) = 2
For n = 4, product of chords emanating from (1, 0) = [sqrt(2)]^4 = 4
For n = 6, product of chords emanating from (1, 0) = 2 *[2*cos(30)]^2 * [2*cos(60)]^2 = 6
For n = 8, product of chords emanating from (1, 0) = 2 * [2*cos(22.5)]^2 * [2*cos(45)]^2 * [2*cos(67.5)^2] = 8
etc. Similarly for n = 10, product = 10.
So, at least for the even n’s, the pattern for the product is 2 times the product of [2*cos(theta)]^2, where theta is a positive whole multiple of 180/n, up to (90-180/n), and inductively I would conjecture that the overall product always simplifies to n.
Note that I don’t remember how to write this formula more concisely, but I think the approach I took was pretty simple. I simply drew the diagram, and I drew right triangles in the upper two quadrants, with their hypotenuse being from (-1, 0) to (1, 0) and one leg being the chord in question. With this, you can find all the chord lengths using simple trig. It turns out that the angles, theta, between the chords and the fixed hypotenuse increase in increments equivalent to half of the central angle. (So, if n = 10, the angles between the chords and the hypotenuse increase by increments of 18 instead of 36.)
Is that helpful? Sorry again my calculus is rusty, and (since I am working from enumerating the examples and inducting patterns) I haven’t quite worked out the odd cases yet. But, I think this approach is simple enough for precalc. I’ll try to think through the odd case and see if it matches this pattern.
@peeterjoot Ah, OK. Back to the drawing board then.
Oh, and for odd cases:
For n = 1, product = 1
For n = 3, product = [2*cos(30)]^2 = 3
For n = 5, product = [2*cos(18)]^2 * [2*cos(56)]^2 = 5
n = 7 involves decimals (a bit hairier for enumeration purposes), so let’s skip it and go to n = 9.
For n = 9, product = [2*cos(10)]^2 * [2*cos(30)]^2 * [2*cos(50)]^2 * [2*cos(70)]^2 = 9
So, the inductive pattern seems to hold for the odd n’s. I used the same simple geometric (right-triangle in upper 2 quadrants) approach I described before to get these. Generalizing the formula for odd n’s, it looks like you need to multiply all the terms [2*cos(theta)]^2, where theta is 90/n + a whole multiple of 180/n. Theta is upper-bounded by (90-180/n).
Again, my calculus is rusty, so if you know how to simplify these algebraic notations above (that I have described in words), please chime in!
By the way, I had made a small typo in the last post, and I’m fixing it here:
For n = 8, product of chords emanating from (1, 0) = 2 * [2*cos(22.5)]^2 * [2*cos(45)]^2 * [2*cos(67.5)]^2 = 8
To help illustrate the simple geometric approach I was talking about, here is one sketch in particular, for n = 10. You can find the angles that are in the diagram because they are 1/2 of their intercepted arc (or central angle). Similarly, all those other right angles near the top are 90 degrees because they intersect an arc that spans a semi-circle along the bottom.
After just doing it numerically i find that the product of the n chords is n!
Now the analytical part…
I didn’t mean n factorial, but the exclamation point was just for amazement!
We can remove the reliance on limits and L’Hopital’s rule from Andrew’s solution by noting that for ,
, 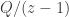 is equal to
is equal to
To find the product of the lengths of the chords, evaluate the absolute value of this at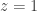 which is
which is
Either way, this is the elegant sneaky fancy-*ss solution that you only think of if you have some experience with a) complex numbers (so you know that you can multiply the lengths of these chords by multiplying the complex numbers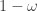 etc. and taking the absolute value), and b) the algebra of the nth roots of unity (so that you know that products like
etc. and taking the absolute value), and b) the algebra of the nth roots of unity (so that you know that products like 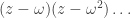 are going to be nicely behaved). I think if I were going to use this problem in a precalc class, I would either a) do a unit on nth roots of unity and give them this problem sometime afterward, or b) let them mess around with trig, using methods like Mimi’s, and come up with a conjecture. Maybe use this conjecture to motivate the study of nth roots of unity? (Driving question: “Why (the hell) did the answer come out so nice? How could we prove it?”) On the other hand, maybe nth roots of unity don’t belong in precalc because they don’t really support a first year of calculus. On the still other hand, lots of traditional precalc content doesn’t either.
are going to be nicely behaved). I think if I were going to use this problem in a precalc class, I would either a) do a unit on nth roots of unity and give them this problem sometime afterward, or b) let them mess around with trig, using methods like Mimi’s, and come up with a conjecture. Maybe use this conjecture to motivate the study of nth roots of unity? (Driving question: “Why (the hell) did the answer come out so nice? How could we prove it?”) On the other hand, maybe nth roots of unity don’t belong in precalc because they don’t really support a first year of calculus. On the still other hand, lots of traditional precalc content doesn’t either.
(Has anyone got a proof that doesn’t depend on all this cutesyness with the roots of unity?)
Btw, Sam, your extension is totally throwing me for a loop because the minute it’s not a circle all my nth roots of unity tricks vanish! Also, I have a question about interpretation of the problem: on the circumference of the ellipse how do I space the points?
a) so that they have equal arc lengths between them?
b) so that the arcs between them subtend equal angles at the center?
c) so that if I squished the ellipse back into a circle the points would be carried to the vertices of a regular polygon?
Ben, I have also been looking for a proof that doesn’t involve understanding of complex numbers, etc.
You can use the law of cosines (due to the fact that every chord forms a triangle with two legs of side=1) along with the double angle identity to produce the following answer (which is in two cases because of the middle “long” chord when n is even):
to produce the following answer (which is in two cases because of the middle “long” chord when n is even):
If n is even you get the product is
and if n is odd you get
These formulas obviously aren’t that helpful, but once we know the answer is actually , this provides a pretty cool identity:
, this provides a pretty cool identity:
So for instance,
 .
.
In particular this gives an interesting formula for the square root of an integer. Does anyone know why this progressive product of sines gives this?
In terms of a trigonometry class, this is a hard problem, but shows how to use the law of cosines and the double angle identity, and provides an interesting identity that should probably get students at least a bit interested in the trigonometric functions, but I will keep looking for a more “basic” way to get to the answer.
Seems to be two different problems/solutions floating around. For clarity sake, I’m looking at the problem where every line segment starts from (1,0) so you end up with a “sun ray” instead of a polygon. I’m also attempting to solve this problem using the tools that a 10th or 11th grader would have (not including my mad latex skills). So nothing more than trig (ideally, no complex plane). We’ll see how that works out, especially since at first I sort of cheated by using polar coordinates (but later realized I didn’t need to do this). Finally, this is purposely written out as my process, not as a nice neat solution.
SPOILER (SORT OF)
I’m going to talk about my process more than my solution, which includes some false paths.
1. Made a t-table to see if there was an obvious pattern I could discern. corresponds with the number of points and
corresponds with the number of points and  corresponds to the length.
corresponds to the length.
The first mistake I made (which I flushed out for longer than I’d like to admit) was to look at the SUMS of segment lengths instead of the product (not as obvious a pattern). Once I was actually solving the right problem, though, this is what I ended up with.
n | l
1 | 0
2 | 2
3 | 3
4 | 4
5 | 5
And not that I needed much more convincing, but because it can be computed only using special triangles…
6 | 6
Ok. I’m sufficiently intrigued.
Next thing I noticed is that the n=6 case is made up of the n=2 and n=3 cases, along with 2 extras (that have a product of 1). More generally, the 30th case will consist of the segments made in the 2nd, 3rd, 5th, 6th, etc cases (ie all the factors). Unfortunately, there’s going to be overlap and there’s going to be some segments you have to add to the 30th case (The segments connected by the points going 1/30, 7/30, 11/30, 13/30, 17/30, 19/30, 23/30, and 29/30 around the circle…ie all the numbers where the GCF is 1 or in other words where the fractions that can’t be reduced). Maybe the geometric mean would help? Who knows. So I abandoned this approach. May be worth returning to at some point…
My next approach was to see if the any of the distance formulas would reduce nicely. In polar coordinates, the distance between two points is (I decided not to include the derivation):
In my case and
and  (my starting point at (1,0) so this reduces nicely to
(my starting point at (1,0) so this reduces nicely to  or
or 
As an aside, this can also be approached using isosceles triangles and sines giving you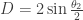 . Along with the previous method, you now have the half-angle formula for sine. That’s kind of cool.
. Along with the previous method, you now have the half-angle formula for sine. That’s kind of cool.
So what I am interested in is the following (I’ll use sines because it’s cleaner and because I now have an excuse to ignore the derivation for the distance formula in polar coordinates):
or
My next step was to see if there was a nice trig identity for this. There is an identity, but it’s not nice.
It gets much uglier for more than 2 terms.
After some pondering, I realized that taking advantage of the symmetry in the problem might help. If you match up the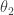 with
with 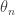 and
and 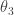 with
with 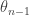 (now realizing I might have wanted to index my thetas differently…oh well), the sums will be 0 (because, for example,
(now realizing I might have wanted to index my thetas differently…oh well), the sums will be 0 (because, for example, 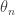 can also be thought of as
can also be thought of as 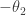 . The difference will just be
. The difference will just be  so each part becomes:
so each part becomes:
If n is even you’ll have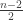 sets, along with the (1, 0) to (-1,0) segment of length 2 (the minus 2 comes from the two points on the x-axis).
sets, along with the (1, 0) to (-1,0) segment of length 2 (the minus 2 comes from the two points on the x-axis).
If n is odd, you’ll have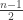 sets and no extra segment to deal with (the minus one comes from the one point on the x-axis).
sets and no extra segment to deal with (the minus one comes from the one point on the x-axis).
Boy, it would be nice to not have all these special cases. Hmmm…
So for the entire thing…
Even case:
I’m going to switch all the cosines and ones. Motivation? Saw some difference of squares lurking. I’ll also combine the 2’s and halves.
If n is a multiple of 4, there is additional symmetries.
etc.
This means that we have some differences of squares and that the original formula can be simplified to
At this point I realized that I could have made it here much more directly by using the symmetry ( instead of using the product identity. Woops. Alas, I guess I now know a new trig identity. Either way, here I am with a bunch of sine squared terms (all the angles in the first 2 quadrants) and a bunch of 2’s.
instead of using the product identity. Woops. Alas, I guess I now know a new trig identity. Either way, here I am with a bunch of sine squared terms (all the angles in the first 2 quadrants) and a bunch of 2’s.
Well, if n is a multiple of 4, there’s also going to be symmetry around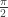 and once again the first and last term, the second and second to last term, etc will be able to be combined to give you:
and once again the first and last term, the second and second to last term, etc will be able to be combined to give you:
or alternatively
Ok. I’ve spent long enough on this that I think I want to post it without finishing…ie I’m stuck :)
Hi again,
I created my own Geogebra applet to investigate the problem with the ellipse (as you have it written I think). The products turn out to be very interesting:
The lengths of the cords are as follows for certain n:
n length
2 2=2*1
3 6=3*2
4 12=4*3
5 25= 5*5
6 48=6*8
7 91=7*13
8 168= 8*21
9 306=9*34
10 550=10*55
So the conjecture would then be
n n*F_n
where F_n is the n’th Fibonacci number. This is not too far-fetched as the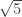 appears in the formula. I would guess there is some proof similar to the solutions for the circle but using a different formula. Just thought people might be interested.
appears in the formula. I would guess there is some proof similar to the solutions for the circle but using a different formula. Just thought people might be interested.
Thanks for posting this problem, there are a lot of interesting things going on.
That’s crazy!
I have to understand this.
Followup a decade later lol.
Japheth Wood and I wrote a paper about it which appeared in the American Mathematical Monthly.
Cool problem. The only partial solution I found that didn’t use complex roots is similar to Mimi’s. The solution uses distance formula:
Choose one of the n points on the unit circle. Its coordinates are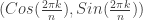 where
where  . Then the distance between that point and $(1,0)$ is, according to the distance formula:
. Then the distance between that point and $(1,0)$ is, according to the distance formula:
So that’s the length of the “kth” chord. The product is then
At this point, I’m not sure if you can solve it without invoking roots of unity. You can definitely simplify it by realizing the symmetry of the situation (so you can narrow it down to (n-1)/2 multiplications) or multiplying it out and using sum-difference formulas (but that’s ugly). Besides that, I’m not sure.
I haven’t read anyone else’s solutions yet.
I posted mine at
I’ve learn some excellent stuff here. Definitely worth bookmarking for revisiting.
I wonder how a lot attempt you put to create any such great informative site.