CalcDave posted some awesome questions to ask calculus students — to get them think of the very large and the very small… and I made a worksheet out of it. For posterity, I wanted to save some of the responses.
The least probable (but still possible) event that you can think of
- Going skydiving with the president
- That I will drop out of high school the day before my graduation
- When I call ‘stop!’ my watch reads 12:00pm and 0.0000000001 seconds
- Mr. Shah becoming a rock star in a band called “Pain in my asymptote”
- A monkey typing a Shakespeare play on a typewriter
- The Boston Red Sox winning the American League East
- All the people in the world dying at one time
- Winning the lottery
- Pauly D not having a date and Snookie beating Jwoww in a fight
- The Situation never having STDs
- A 7.8 (richter scale) earthquake in NYC
Largest number
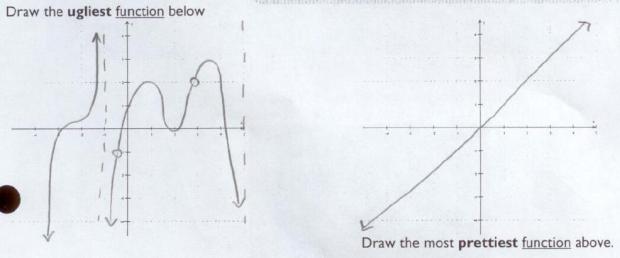
Draw the ugliest and prettiest functions
I asked the last question about pretty/ugly functions, because I assumed that most kids would draw continuous everywhere and differentiable everywhere functions. And for the ugly ones, those would be violated. We’d have asymptotes, holes, and non-differentiable points. My assumption was realized. So we’re going to have a talk about the aesthetics of math, and coming up with mathematical descriptions for “beautiful functions.” I want them to think about continuity and differentiability, without knowing the terms explicitly.
Now it’s going to be great. Whenever we start talking about infinity or infinitely small, we’ll have some juicy stuff to dig into — stuff they’ve mulled over. Even today, I was talking about watching a video of someone diving and pausing it. And then going to the next frame — and infinitesimally small amount of time afterwards.
We also zoomed in on a point on a graph a huge number of times. An almost infinite amount of time.
And the thing on the screen turned to look closer and closer and closer and closer to a straight line. But it never became a perfect line. Every point on the screen, as you zoom in, gets infinitely close to lying on a straight line. But it won’t ever be a straight line.
So great conversations. We’ll expand them as we continue. Especially how every (continuous) curve is an infinite number of infinitely small line segments joined together.


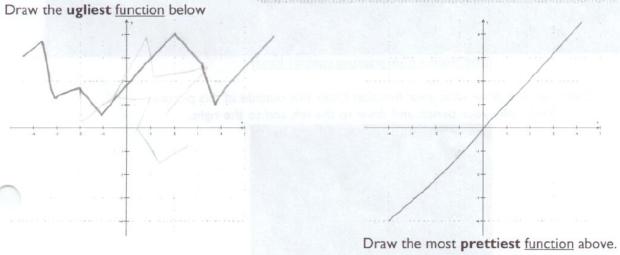
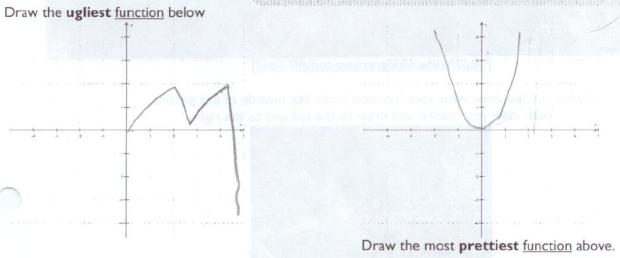
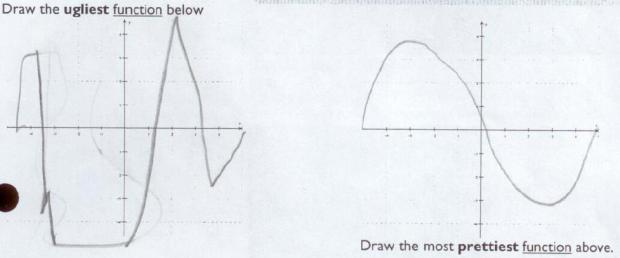
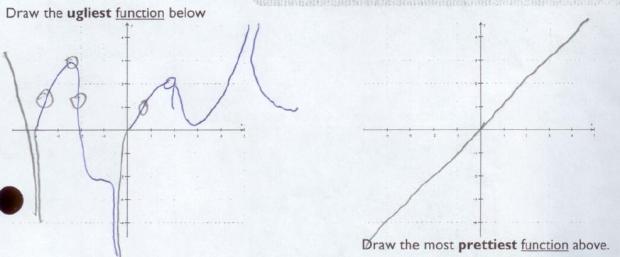
Yay! I love your extensions.
Maybe this should become a “walk-off” where we repeat and add an embellishment each time. Maybe we can even get Bowie to judge.
The whole fill in the gap question is good when talking about limits… I started referring to it already today.
Love this train of thought with math. Will have to adapt it for my elementary kids.
I am totally stealing this for my Calc kids next week. I am curious about their responses. Love this!
This almost makes me wish I taught calc. :) I’ll have to pass this on to my colleague who does teach it.
Also, Sam, I hate to be the grammar police, but the “most prettiest”?
I don’t think you hate it (*grin*). But yes, that was on purpose. It’s cuter that way. The point of this sheet is to be cute.
Given the name of your blog, I wonder if it makes sense to (gradually) introduce some wild functions… 1 at rationals and 0 at irrationals, 1/q at rationals and 0 at irrationals, and the prettiest of them all – Conway’s base 13 function, horribly discontinuous but satisfying the mean value property BIG time. With some patience it should be possible to get students to follow the definition (though this may take time), and see why it obtains every value on every interval, small as it may be.
It’s actually easier to define than a continuous, nowhere-differentiable function, and it’s really pretty!
I love that idea. I actually already spend about a day talking about the function y=sin(1/x), and ask the question: what’s the limit as x approaches 0. I have students investigate it with their calculators (graphically, with tables, etc.) and make observations. Then we mathematicize our observations, and come up with a conclusion – as to WHY the function doesn’t have a limit as x-approaches 0.
That’s about as far as I can go. I don’t think my kids would really appreciate the 1 at rationals, 0 at irrationals function (because they don’t really have a good sense of even what rational and irrational are). We would get lost before even starting. At least I suspect so. I wonder if there is some guided worksheet/activity that would take us through it…
These are great. Be sure to let us know when the debut album releases.
Check this out:
Found here: http://twentytwowords.com/2010/10/20/amazing-shadow-sculptures/
Guess whose calc classes are going to see a pretty picture today?
MINE!
Thanks. This is awesome.