I am just finishing up my quadratics unit in Algebra II. We spend a lot of time on quadratics, doing everything from factoring, to completing the square, to the quadratic formula, to all sorts of graphing, the discriminant, 1D and 2D quadratic inequalities, quadratic linear systems, systems of inequalities, etc. Tons. And we didn’t even get to do the project I enjoy involving pendulums and quadratic regressions. Le sigh.
I’ve posted much of my quadratics materials before, but I thought I’d share some new/updated ones. I’m a bit exhausted, so forgive the shortness of my descriptions.
1. My Vertex Form worksheet was motivated by my frustration with students just memorizing that 
[.doc]
2. My Angry Birds activity was inspired by Sean Sweeney, but modified. I had taught students how to graph (by hand) quadratics of the form 
If I’m teaching Algebra II next year, I want to ask if I can get rid of quadratic inequalities or some of the other more technical things we do, and make an entire unit/investigation on using geogebra and algebra and angrybirds to investigate quadratics.
3. My discriminant worksheet is below. It worked okay, but students still didn’t quite understand the difference between 
[
[doc]
4. Finally, below are my attempts to get students to better understand quadratic inequalities. I started with a general sheet on “visualizing function inequalities,” and then I made a guided sheet to bring more detail to things. I found out that students didn’t quite understand the meaning of the schematic diagram we drew, nor did they understand why to solve 
[doc]
[doc]
C’est tout. With that, I’m exhausted and going to bed.
Continuous Everywhere but Differentiable Nowhere 
As I was reading your #4 on quadratic inequalities, I too had to pause for a moment and figure out how the 2D graph played into the 1D inequalities… and then once my brain cleared, the more important question arose of “Why did this confuse me at first?”
I think the answer lies in Algebra 1, where we teach linear inequalities. When solving a 1D linear inequality, we simply follow the same steps as solving a linear equation (with the one exception of ‘flipping’ the inequality symbol after mult/div by a negative). The graphs are only introduced when the inequality becomes two-dimensional, and of course, then the solution is a shaded region on the graph and not a shaded segment.
Ideally, we should introduce linear inequalities with algebraic and graphical methods supporting each other, but it’s easy for a student to ignore the graphical (even if the teacher doesn’t) because the algebraic works so seamlessly. Nevertheless, as an Algebra II teacher, you have very little control over what they learned in Algebra I. So I think it is important to begin where they are: quadratic inequalities can also be solved algebraically, as long as your solution method involves a series of inverse operations (mult/div by negative still means to flip the sign and now, we also have to employ absolute value rules when taking roots). This will require completing the square first, in order for the inverse operations method to work, which as we know, can be tedious, and falls apart as soon as you get to polynomials of higher degree.
I think the big idea in the quadratics/polynomials unit is that the methods we have used before to solve problems start to fall apart here… because the conditions are not quite right. So we have a couple of choices: force the problems into the correct conditions, or come up with some new methods. Coming up with new methods can seem a little more palatable once we’ve experienced how difficult it can be to force the old conditions.
Next year, I’d suggest starting the inequalities with a progressive worksheet like this:
1. (3x-5)/2<0
2. |x/2+7|-3<0
3. x^2 – 4 <0
4. x^2 -4x +3 <0
Make them struggle with their algebraic methods, then show them how to perfect their algebra. Finally give them the graphs (if someone hasn't already come up with them already!) and show them where they can 'see' their solutions on the graphs.
They will say 'Why didn't we learn it this way in Algebra I?!" To which you can say, "You probably did, but then you found the graphs complicated and the algebra easy." Now it's a different story.
What is the structure of your Algebra II curriculum? In my state Quadratics is a semester 1 topic and we cover everything you listed except for inequalities and quadratic systems. At this point in the year we’re knee deep in logarithms and have done graph transformations to death.
Fall: Multi-Step Equations, Linear Functions, Absolute Value, Linear Systems, Matrices, Quadratics
Spring: Polynomials, Logs and Logs Equations both standard and natural, Rational Functions Graphs and Equations, Radical Functions Graphs and Equations, Conics
Click to access Algebra%20II%20Curriculum%20Outline.pdf
I used your Angry birds geogebra lesson yesterday (thanks!) and I have a couple questions.
1. How is the “c” slider calculated? The students noticed it didn’t match the equation on the left side.
2. Whenever I turned on my LCD projector, the sliders would disappear…even when I tried my Mac laptop and pc desktop. Ever heard of this?
Hihi-
The sliders don’t directly correspond to the quadratic on the left. I wanted the kids to start making connections between the sliders and the equation…
so the equation on the left is actually: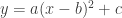
So as they drag b, the quadratic goes left/right; as they drag c, the quadratic goes up/down, and a of course controls the narrowness/wideness and whether the quadratic opens up or down.
What they noticed, besides that, is that the a slider corresponded to the coefficient of the x^2 term, and the b and c slider corresponded to where they found the vertex to be (the x and y coordinate). [That’s why I had them pinpoint the vertex.]
Hope that helped.
Sam
thanks!