One of my multivariable calculus students did her final project based around a book we read and discussed in class. It is called The Calculus of Friendship by Steven Strogatz. In it, the author writes each chapter about his own life and relationship with his former calculus teacher through the lens of some mathematical puzzle or concept.
My student wanted to do something similar, exploring her her multiple identities with her mathematical experience through the lens of multivariable calculus concepts. With her permission, I am putting up her three chapters here. It was a powerful experience listening to it as she read it aloud during her public presentation. I entreat you to read it. And although it may seem strange, there are many parts of it that are worth standing up and reading aloud. If you do that, you can inhabit my student’s voice for a while and really hear what she’s trying to say.
***
The Friendship of Calculus: A Girl’s Journey Into the Unwavering Depths of The Third Dimension
by Brittany Boyce
***
Chapter One: The Fourth Dimension
The fourth dimension as described in the dictionary is “a postulated spatial dimension additional to those determining length, area, and volume.” The key word in that definition is postulated. The fourth dimension is not something we can see, hear or touch, it comes from our imagination. In the times of early human life, the Mystics saw the fourth dimension as a place where spirits resided, since they did not inhabit our 3-dimensional world and were therefore not limited to our earthly confines. Albert Einstein, in his theory of special relativity, called the fourth-dimension time, but also concluded that time and space were inseparable. But what truly is the fourth dimension? In life, we try to make meaning of the world, what it will bring, what it will mean, how it will help us grow or not, and how it will change. Although we have a certain plan on what we want our world to look like, it is not something tangible that we can hold on to or grasp. The 4th dimension is something we can only imagine. We use the 3rd dimension, what we know and live through to help us envision the 4th. We assign colors and densities to certain points in space, and that helps us paint a picture that we can live with, but we are never truly satisfied.
In 1884 Edward A. Abbott, published a book about the problem of seeing dimensions that are not our own. In “Flatland: A Romance of Many Dimensions,” Abbott describes the life of a square living in a 2-dimensional world, which means he lives with triangles, rectangles, circles, and other two dimensional creatures, but all he sees are other lines because everything is flat. When the square finally has the chance to visit the third dimension with the help of a trusty sphere, a new world opens up to the square. Yes he is a shape like his 3rd dimensional counterparts, but he never took the chance to step out of his world and never sought to understand other worlds because he was never encouraged. At first, the square did not have the ability to comprehend the 3rd dimension, because for his whole life he only knew two dimensions. When the sphere takes the square out of the 2nd dimension, the square is finally able to see that there is a lot more to the world than just flat shapes like himself. The square was able to learn that other shapes have depth, color, height, etc. and because he was so amazed he turned to the sphere and asked what was beyond this dimension. The sphere, like the square, was appalled, unable to comprehend a world that wasn’t his own.
In this way, the sphere is like each and everyone of us. We are unable to comprehend other worlds, simply because we haven’t lived in other worlds. Our levels of privilege and different experiences explicitly prohibit us from knowing what each other’s lives are like. But does that mean we shouldn’t try? Does that mean we should just sit down and not try to understand anything simply because it is different from our experience? The answer to that question my friends, is a simple no.
∫ ∫ ∫
It was spring of junior year 2016 and I was sitting with my dean at the time, Mr. Brownstone, in his office going over my course registration. Now, this was it. This was the end, the last course registration I would ever have to do, the icing on the cake that would make me and my resume look appealing to the college of my dreams.
We were going over each class to make sure they looked okay, english looked good, history looked good, languages looked good, and art looked good. The only problem was if I was going to decide to jump into the deep end that was Multivariable Calculus. At first when I heard that Multivariable Calculus was an option I avoided that conversation like the plague with all my previous math teachers.
“You’re taking Multi right?” Mr. Brownstone said.
“Can I take Math Apps instead? They’re both different types of advanced math right?” I replied with a slight chuckle. He looked and me and laughed and replied with a hard “No.” There was no way he wasn’t letting me take Multivariable Calculus, and there was no way he wouldn’t make me step up to the challenge. As a kid who was already succeeding, I did not see the point in taking something extremely hard, but I went along with it anyway.
See that’s the thing about Mr. Brownstone and many other faculty members at Packer. They look out for you by pushing you to your limits and although in the moment you hate them, it’s always worth it in the end. Multivariable Calculus had already had its reputation of being a class, that would really “challenge you,” to put it nicely. Mr. Shah also already had a reputation of being one of the hardest teachers in Packer, so just thinking about this class was making my stress levels rise.
As a junior going into what would be the second half of the hardest year of my life, I didn’t think I was ready for this level of mathematics. I had always prided myself on being good at math and I enjoyed the subject as a whole but all the new variables, operators, and symbols in calculus had opened the door to a whole new side of math that scared me to be honest. Not that an integral sign is physically scary in anyway, but I was scared of the fact that I might not be able to do it. I was scared of needing help because growing up I was taught to be independent. Help was a foreign concept to me because I’ve always been told that based on my skin color no one was willing to help me and so I always had to fight for myself.They had always taught me to be independent because independence was power, and power was success.
Multivariable Calculus had always been a puzzling topic to me. What is it? I still couldn’t tell you. I was already confused by the addition of the alphabet, Greek and English, into the mathematical world, so when I heard that there could be multiple variables added into equations that I would soon be required to solve, I was even more worried. I remember thinking to myself that Mr. Shah would be too hard of a teacher for me and that the material would be too confusing. There was a part of me that thought that I would lose my status of “intelligent” and that I would let down all the people who told me I could be successful regardless of my background. In taking this class, I felt a certain pressure to do well as a poor, young, black, gay woman because not many others like me had this opportunity to study at such a high level in high school. Going to a place like The Packer Collegiate Institute, where I was one of few, always reminded me of my duty to the marginalized communities.
This type of math, meaning calculus, had always felt like a very distant topic to me. I never could picture myself being a “mathematician” because even though I was passionate about math and I had always been good at it, when I looked in the mirror, I never saw a mathematician.
∫ ∫ ∫
So it was September of 2016 and my first day of Multivariable Calculus with Mr. Shah had finally arrived. I had no idea what to expect and I was scared out of my mind. It was my second day of classes as a senior in highschool. The pressure was on. I had a chance to prove that I could be as great as everyone thought I could be. So here was my shot, my ticket to the big time academia.
Overall, looking at my new math teacher, Mr. Shah, he didn’t look so intimidating. However, his reputation still preceded him. See that’s the thing about Packer teachers, there are some that you can’t mess with. Some that are so passionate about what they study that they try to imbue you with that same passion in the form of school work. They expect so much of you, and give you so much work to better you, that you can’t help hate and respect them for it.
Every Packer upper schooler knows who I am talking about. Firstly in the sciences, there is Dr. Lurain, an exceptional chemistry teacher who often appears and often is very serious, but will light up and burst out in laughter in appreciation of a good chemistry joke. Next, in the languages there is Mr. Flannery, an inspiring Latin teacher who pushes his students to the breaking point every week with his famous tests. You will always catch one of his students learning lines, memorizing vocab, or reading some famous classical story. Mr. Flannery is no joke, but he has a devout dedication to each and every one of his students. The list goes on and on, but Mr. Shah was one of those teachers. Students told me how they were required to write essays on their tests or be so thorough in their answers to get full credit. But, he didn’t have the demeanor of a mean and strict teacher, he was very passionate about math and he didn’t look like he planned to intentionally make my life a living hell.
∫ ∫ ∫
In the first few days of Multivariable Calculus with Mr. Shah, I remember thinking “okay, come on hit me! I can handle it.” I was expecting some complex problem that I couldn’t handle or some other problem that required, some “higher math” that required prior knowledge I didn’t get a chance to grow up with. Instead, Mr. Shah nurtured us, all of us. He taught us not to be scared of Multivariable Calculus. He taught us that we were prepared for 3-dimensional calculus, and the third dimension was just a step up from the second dimension. He made us aware that we already fought hard enough through Calc I & II with Mr. Rumsey, which was a battle of its own, to be sitting here together taking the same class. He never said it was going to be easy, but he made us feel like we were prepared from the bottom up. But, this comfort and reassurance is not something everyone in the world has the privilege to have.
At times, going up a dimension can seem scary. Most often, in our world things can be complicated enough, which causes us to forget that there are things that are higher than ourselves and more important than ourselves. If you’re like me, you use the fact that two-dimensional calculus was already hard enough, so why study 3-dimensions? Why go beyond what you already know? What’s the point?
The point wasn’t to solve the problem right every time or to be able to understand the most complex things first. It was to be willing to take that step into the unknown in the first place. I had an amazing opportunity to try to understand a world that didn’t necessarily welcome me with open arms. I wasn’t lucky because I had the intellectual ability to take Multivariable Calculus. I was lucky because I was one of few students who had an instructor that made me feel like I could understand the higher maths. Not many kids my age have the ability to study the higher maths, or to even believe that they could study the higher maths, especially students of color, women, and LGBTQ+ students. Today’s education system lacks mentors that have the ability to push kids in the right direction and to make them believe in themselves regardless of their social status. What is unique to my experience is that as a woman of color, low socioeconomic status, and who is proud to say that she is a part of the LGBTQ+ community, I had people around to support me. There was never one time I felt that my peers or teacher didn’t think I was worthy enough to be there taking that class because of my gender, race, sexuality, or socio economic status.
However, although my reality was brighter and more positive than other students who share my identity and do not have the same support system I do, I cannot just be grateful and move on with my life. I must think about those who have to fight harder, speak louder, and do better than I do to hold their place in the classroom and the community of the higher maths. I must bring attention to their fight even though I only know my own.
Chapter Two: Line Integrals
A line integral is essentially integration of a function along a curve. But, that means nothing to most of you. On each curve there are an infinite number of points that trace the path of the curve, determining what it will look like, how it will behave, and how it can be analyzed. Not each point is worth more than another in value or in status, but each plays an integral role in defining the curve. Let’s just say, all points are created equal. But what does that curve really mean? What can it do for us and what can we do for it? Sure it can be pretty to look at or cool to trace, but it all means nothing if we can’t make something out of it or give meaning to it.
That’s where our friend the line integral comes in. To many, it looks like a weird “s.” To my readers, three of these majestic creatures in a row means that I am switching directions or switching to a different moment in time. But to a mathematician, the line integral gives meaning to the curve. It takes the path traced by the infinite amount of points and cuts it into infinitesimally small pieces and adds it all together into the culmination of a single amount, quantity, and meaning. The line integral represents the culmination of everything we’ve been through and the addition of all those infinite moments into one big picture called life. But, while you may have all the pieces and the trajectory, solving the line integral and finding the meaning behind the trajectory, will not always be easy.
Often times, in school we as children are set on a given path or a chosen trajectory, let’s call it f(x). We are given a curve C, and we are told to follow it. We get the grades, play the sports, and be the children our parents want us to be. But what does it all mean when we have hit all the points, traced the path, and completed it? What is it supposed to mean? How are we supposed to evaluate our lives when we haven’t even begun to make any choices for ourselves? And how are we supposed to deal the the fact that we may never make meaning of our chosen path even though we might have all the tools?
The creators of calculus dared to confront this problem through math, because of course, it was the only option. To them, doing the work, solving the integral and making meaning of such a path, was more important than perhaps what the integral meant numerically. Frankly, to be the most cliche, it’s about the journey, not the destination. Not all integrals are meant to be solved in the most complex way or with calculus; sometimes it only takes simplest geometric proof or the simplest meaning of life that can propel you in the right direction, or help you move forward in the problem.
Do you ever wonder how long it takes to change your life? What measure of time is enough to be life altering? Is it four years like high school? One year? A 2-semester calculus class? A semester long, history course? Can your life change in a month? A week? A single day? We’re always in a hurry to grow up, to go places, and get ahead. But when you’re young, one hour or even 50 minutes can change everything.
Through integration, a curve becomes a series of tiny straight lines, working together towards one common quantity. Through integration, life becomes a series of tiny moments working together towards the culmination of you and what your life means. However, sometimes it may be hard to make meaning of a certain time in your life. Sometimes that moment may be unsolvable and that can be frustrating. But, the important thing to remember is that each infinitesimally small piece or small moment works to affect the meaning of your life. Each small experience adds something to your journey.
∫ ∫ ∫
I had made it through the first semester of Multivariable Calculus feeling like I could actually pursue mathematics in college. But, I wasn’t completely sure what helped me get here. There was some small moment along my path, where it just clicked. There was something about the elegance of Multivariable Calculus that caused me to light up during every class. Surely there were days that I was tired and defeated, and felt that I could not take anymore of Mr. Shah’s high expectations; But, something about the math itself always brought me back to that stillness I felt. The stillness that was almost calming at the sight of an elegant proof or after spending time doing hard rough algebra, fighting and wrestling with exponents, variables, and symbols to finally get an answer. I didn’t know it then, but that stillness was my ability to feel passionate about math. I had a willingness to understand the concepts behind the algebra I was doing, and had come to appreciate the conceptual approach rather than the hard hitting, laborious algebra I was used to my whole life.
For the more complex conceptual solutions, sometimes I felt cheated, when the very complex parts of the problems were reduced by simple geometric approaches. I saw the immense power of calculus, and I didn’t want it to be reduced or lessened by geometry. There was something about putting my head down and jack hammering through the hard work that always pleased me, but I soon learned that it wasn’t cheating, nor did it lessen the power of calculus in any way.
One simple solution to a complex integral we often faced in class was the integral of cos^2(x) from zero to kπ, k being a multiple of ½. Now for all you mathematicians out there, you know that this integral is no joke. There is no simple u-substitution or power rule you can use to solve this, it must be solved with integration by parts, which is a method that requires some of that “jack hammering” I loved so much.
The proof of ∫ cos^2(x)dx using integration by parts, goes as follows:
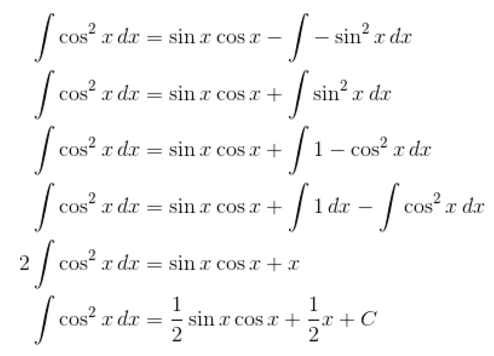
Using this integral, the area under the curve on the interval 0 to π/2, makes the integral equal to π/4. While this solution did take intuition and elegance, such as turning the ∫ sin^2(x)dx into ∫ 1 – cos^2(x)dx. Then, adding the ∫ cos^2(x) to both sides to make the proof simple algebra. We learned to tackle complex integrals like this using integration by parts in Calculus I & II, but 3-dimensional calculus builds on 2-dimensional calculus, so complex integrals always popped up in daily problems. I admired the hard work that calculus required, and the instincts that one could gain from solving such problems, but let’s be real, no one is going to remember the solution to a random integral because one random integral is not that important to all of math. So the question we’re faced with is do we fill our minds with random memorizations of quantities representing areas under curves or do we find another way to remember?
One day, Mr. Shah gave me and my fellow peers a new tool to add to our mathematician’s tool belt. He gaves us geometry. He took us back to our roots and showed us that sometimes simplicity is the ultimate sophistication. So we tackled the same solution.
What is ∫ cos^2(x)dx?
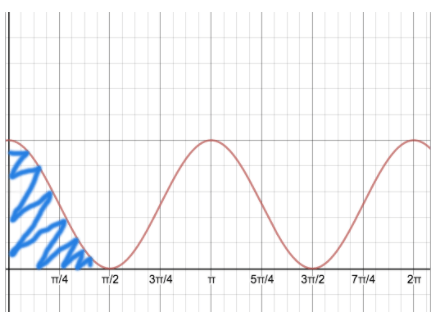
We were essentially tasked with finding the area shaded above. Sometimes when you’re in the middle of solving a problem, and this integral pops up, you can’t result to algebra every time. Sometimes the matter is too urgent and the problem can’t wait for you to do all this algebra. So Mr. Shah showed us one single shape that would change the way we would approach any integral for the rest of our math careers.
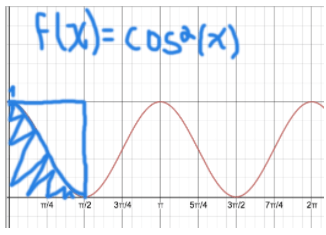
Now look closely. The area under the curve is equivalent to exactly ½ the area of the blue rectangle. Now the graph tells us that the length of the rectangle is 1 and the width of the rectangle is π/2. That makes the area of the rectangle π/2 • 1 = π/2, making half the area of the rectangle π/4. BOOM. One complex integral simplified with the power of geometry. This proof amazed me. I was astounded by the elegance of such a simple solution. I mean a seventh grader could do this.
∫ ∫ ∫
Calculus was never meant to be unreachable. Renowned mathematician Edward Frenkel once said, “mathematics directs the flow of the universe, lurks behind its shapes and curves, and holds the reins of everything from tiny atoms to the biggest stars.” The beauty that math holds has become a privilege unreachable to those who are marginalized everyday for their skin color, race, and sexuality. Everyday students of color and women are told that they cannot or should not see this beauty, the beauty of math is held from them until they climb and fight to the point where they are so bruised, broken and beaten that they give up. There are increasingly low percentages of black and Latinos in high-paying, high-status jobs in finance, science and technology. Since perceived intelligence in the higher math communities are increasingly influenced by racial prejudices it is getting harder and harder for students of color to believe that they can be something more than the stereotypes. Fundamentally, this is a question about power in society.
Being a student of color who had to claw tooth and nail and go to highly selective programs to even be in a place like Packer, I have experienced that loss of a love for education. Being a black girl who was able to show her intelligence at such a young age, I was set on the path to success. Do your school work, get a good job, be successful. But at the time, I didn’t really know what it meant to be successful. I still don’t know what it means. Most of the time, success is dependent on whether or not I beat the system. I was never told to do what makes me happy. I was told to do what makes me money. I never had the privilege of growing up studying what interested me, or what I was passionate about, and I never knew that having the chance to delve into European history or a new language was a privilege. I was too busy preparing for survival. I was busy getting a head start on the material I needed for the future, so the pressure and the rigor of a predominantly white and male setting wouldn’t defeat me.
There are kids out there who don’t get to enjoy and love knowledge because they are not taught that knowledge is beautiful, they are taught that knowledge is power, and that power is the key to success. Academics never become leisure activity because survival is more important than leisure. They are set on their own path, and asked to make meaning of that path without loving the path in the first place. At the end of their trajectory, they are left at a crossroads, choose another path that they truly love with the possibility of failure or never love a path at all.
Chapter Three: Path Independence
Path Independence shows that the value of a line integral of a conservative vector field along a piecewise smooth path is independent of the path; that is the value of the integral depends on the endpoints and not the actual path C. Now wait a second, am I hearing that vector calculus thinks that it’s about the destination not the journey? Frankly, I don’t blame the creators of this theorem. Most of our world thinks life is path independent. People think that they can see past their privileges and just go on with their lives and that every accomplishment they achieve is independent of a third party. But is our world truly conservative? No pun intended. Do we live in a world where, as one of my favorite bloggers puts it, “instead of recognizing our unfair privileges, we just build walls around us and project out way of life as normal. Any story you tell about how you got where you are that doesn’t include land theft, profiting off of forced, unpaid labor, illegal occupation, murder, assault, theft, psychological and physical warfare, exploitations, and a culture of complicity is, you know, a lie.”
If it is then what’s the point of me fighting so hard to hold onto my passion for mathematics? What’s the point if my journey, which might be ten times harder than someone else’s is recognized in the same or even a lesser fashion than someone who got to the same endpoint. Isn’t there supposed to be beauty in the struggle? Value in someone’s journey? What’s the point in finding the meaning of your path if it is weighed the same as everyone else’s path who started and finished at the same places you did? How are we supposed to try to learn and value the experience of others if we just value where we’ve ended up? Does this mean that the situation you are born in, something that you can’t control, has some type of influence on the overall meaning of your path? It shouldn’t.
∫ ∫ ∫
The problem of the conservative vector field that is our world always had a place in our Multivariable Calculus classroom although we sometimes didn’t know it. Every Day 4, when we had class for 90 min, we would hold a book club. Mr. Shah would assign us a different piece of literature to read regarding math, whether it was Flatland by Edward A. Abbott, or The Calculus of Friendship by Steven Strogatz, or Love and Math by Edward Frenkel. As a senior, already up to my eyeballs in work, I disliked him for giving me this reading on top of all the math problems he had already assigned me. I never knew it then, but what Mr. Shah was doing was important work. He was showing us what is was like not to be path independent. He made us value the stories of the mathematicians before us, so that we could know how hard it could be for the person sitting right next to us to be successful in the mathematical community. He made sure to make us feel the responsibility we had to the ethics of the math community. We discussed the politics of math, the religion of math, and the inequities of math every week.
He showed us that while learning the material itself was important, the story behind the material is just as important. In life and in math, there are multiple approaches to solving problems. Often times in math class, Mr. Shah highlighted when two students had different approaches to the same answer and would even have them write it on the board for the whole class to experience. Each approach would have something different. Maybe a trick, a new tool, or even a slight adjustment. When I thought about the way a problem was solved, I never really saw the value in the different approaches, all that mattered to me was that the same answer was achieved.
∫ ∫ ∫
In my last quarter of my Packer career and a Multivariable Calculus student, we returned to pure learning. We watched a series of lectures, which was considered our preparation for college math and the whole host of difficulties that would come with it. As the time was winding down, and I began to think about what my final project would look like, I admired Mr. Shah for making us do something that we were interested in and that was meaningful to us. I had never gotten the chance to do so, while still preparing for “survival.” Once again, I hated all the stress and work it brought me. But, I was very grateful that I had gotten a chance to make meaning out of my experience. While the culmination of my mathematical trajectory or “path” at Packer was not completely numerical or quantitative, the experience of finding meaning through math has been life changing.
Math is beautiful, and I only hope that seeing this beauty no longer becomes a privilege in this world, but a necessity. Everyone deserves to believe that they can be passionate about something and not be deemed a failure. No kid should have to carry the weight of their struggle alone. We must not be path independent, we must be aware of the stories that are around us.
Brittany: this is amazing. Thanks for letting Mr. Shah share it. You write with math understanding and even more beautifully about the people.
How beautiful. Mr. Shah was as lucky to have you as a student as you were to have him as a teacher. Thank you for sharing so articulately and honestly.
That’s some good stuff there.
I’ve been thinking of you quite a bit this year. After over dozen years at title 1 schools, I’ve ended up at a small school that is aimed at nurturing bright kids like yours (though starting at middle school – we’re expanding into high school starting next year). The challenges are different, but they’re still there.
Thank you for still giving me stuff to think about over a dozen years into this job.
I heart you!
One of my favorite things about this online math community is that I can get ideas of people at very different schools with different problems and different populations (and vice versa). It shows that although much of teaching is contextual, there are also some things that are pretty universal!
When I see what comes out of what you do as a teacher, I am humbled, I am jealous, I am spurred on to go even further in my own teaching. This coming year is again Alg I, but with an additional audience: mild math. I will be team teaching to first time 9th graders. I will probably have a class of repeaters, and this new class: students with tested ranges of 65-75 or so. You and the writings of this young lady make me want to infuse my students with a love for math, and an understanding of their journeys. Wow. Just wow! I cannot wait for August!
I think that you are probably imagining a very different teacher than who I really am. So *please* don’t be jealous/humbled. You can tell even from the post above that I am scary/intimidating to them. Your mild math class sounds so challenging, and exciting, both! I know you probably know of cheesemonkey, but she works with so much kindness and love with diverse populations. If you don’t, check her out here: http://cheesemonkeysf.blogspot.com/ and on twitter @cheesemonkeysf … and I can give you her email if you want to chat with her. I think some of her strategies for classroom talk and restorative practices might be of interest for you, if you don’t already know about them.
Always,
Sam
I do love what she does, but I did not know which classes she worked with specifically. Thank you for giving me that information. I will go back to her blog with an eye to my new classroom population. I love this community. It has made me a better teacher, for sure.
😊
This is beautiful. I hope she continues to have good math teachers who make her feel accepted as a person while helping her grow intellectually. If she doesn’t know about them already, please share http://www.mathematicallygiftedandblack.com/ and https://www.edgeforwomen.org/ with her.
WOW!..that’s all i can say!.. i’ve learned some serious stuff..thanks to you!
btw i have just started out a blog about intuitive phenomenon iv’e observed in my daily math and science classes! (Of course it has to be calculus)….
Be sure to check it out!.. I would definitely love to have any suggestions or views you would have on it!.. Thank You! :)
https://cosmicintuitions.wordpress.com/
P.S Student on a quest to understand this universe!