Like in my last post, I want to share a math problem I was working on for a summer professional development I’m doing. This was part of the problem set that the PD organizer Justin Lanier wrote up. The problem is outlined here:

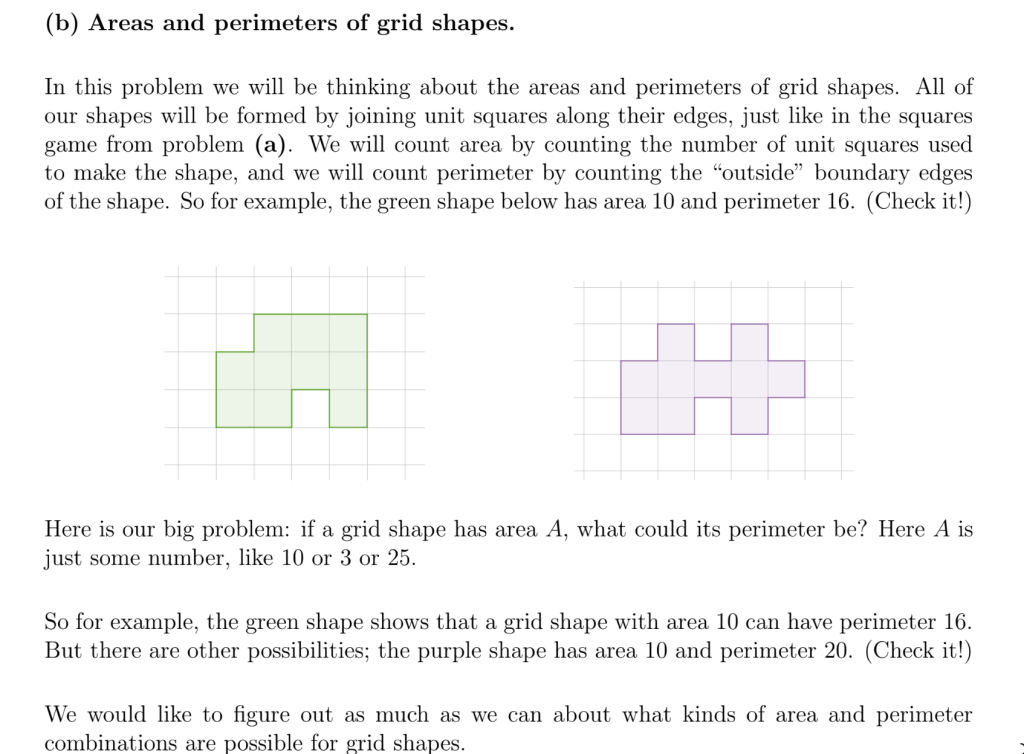
As part of this professional development, we started filling in a spreadsheet with various areas- perimeter combinations we could create. This is a screenshot of collaborative sheet we came up with:

I played around with this problem for hours and hours. I decided I wanted to focus on this question: If you have a given Area of n, what is the Maximum Perimeter you could get, and what is the Minimum Perimeter you could get?

I was relatively easily able to prove that for an Area of n, that the Maximum Perimeter you could create is 4+2(n-1). Here’s the argument in a nutshell. Each time you add on a new square to an existing figure, you either are adding 0 to the perimeter, 1 to the perimeter, or 2 to the perimeter. (This is easy to show.) So to get the Maxmimum Perimeter, you want to be adding the most to the perimeter each time. So if you start out with a single square (n=1) with a perimeter of 4, each time you add a square, you’re adding at most a perimeter of 2 to the figure. One easy way to create this figure is to just add squares like this:

This is where the 4+2(n-1) comes from. You start with a perimeter of 4, and add 2 every new square you add to it.

It took me a while to figure out the Minimum Perimeter. I am pretty certain I have it, but I’m still working on proving it in an airtight way.

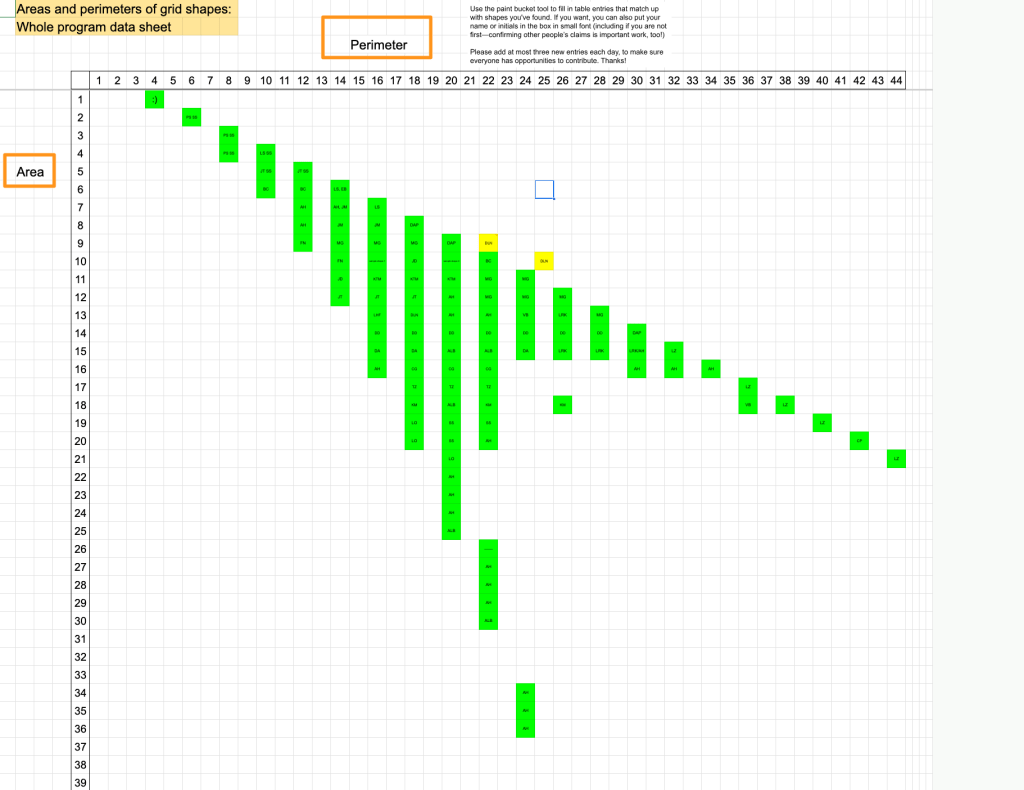
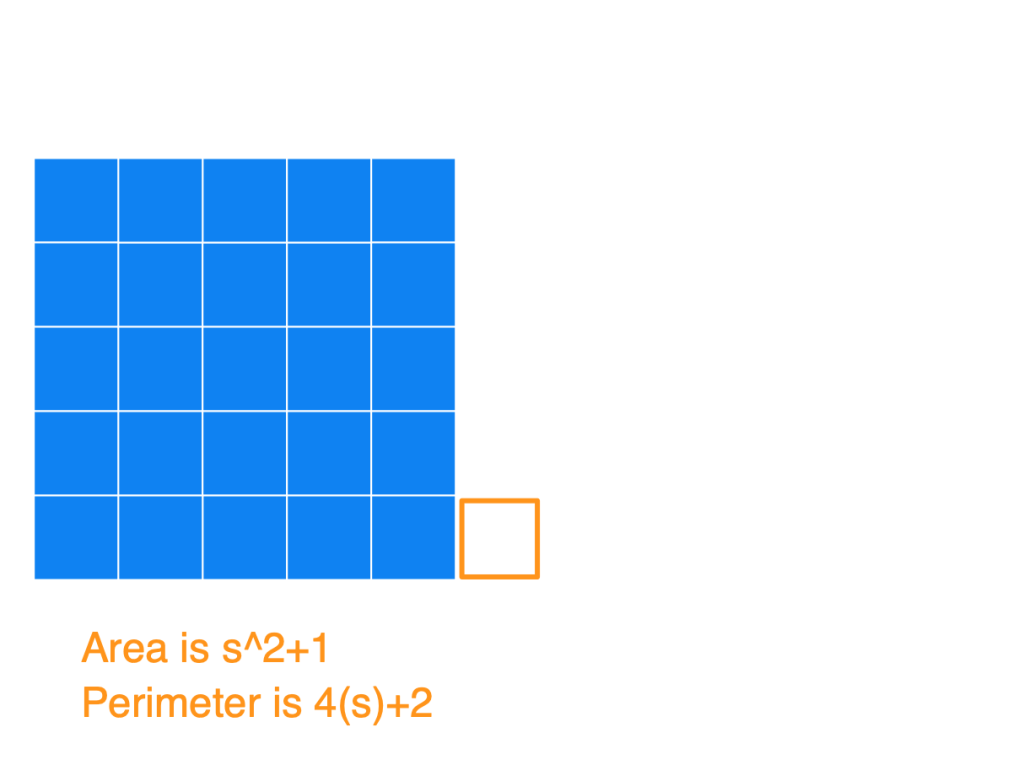
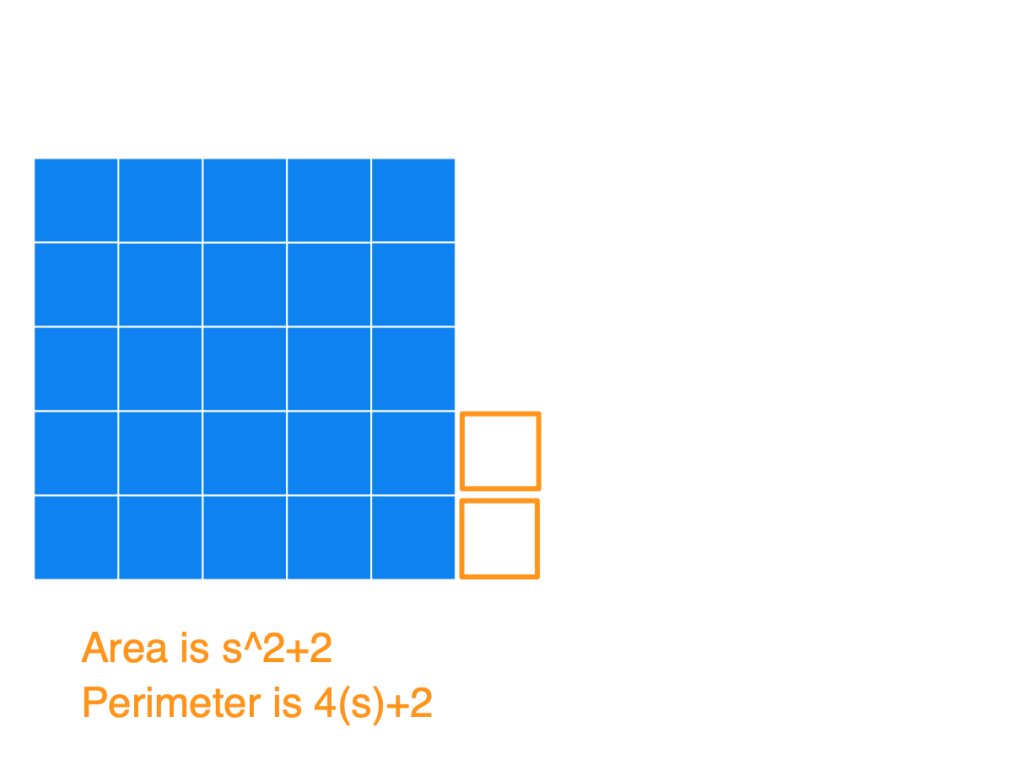
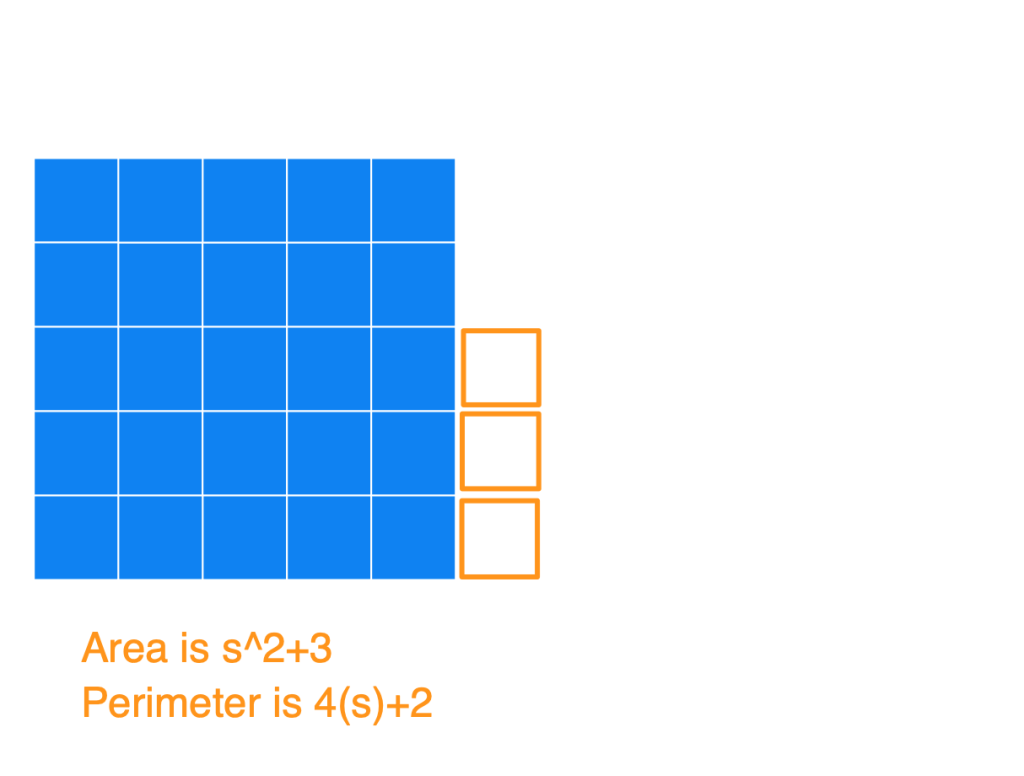
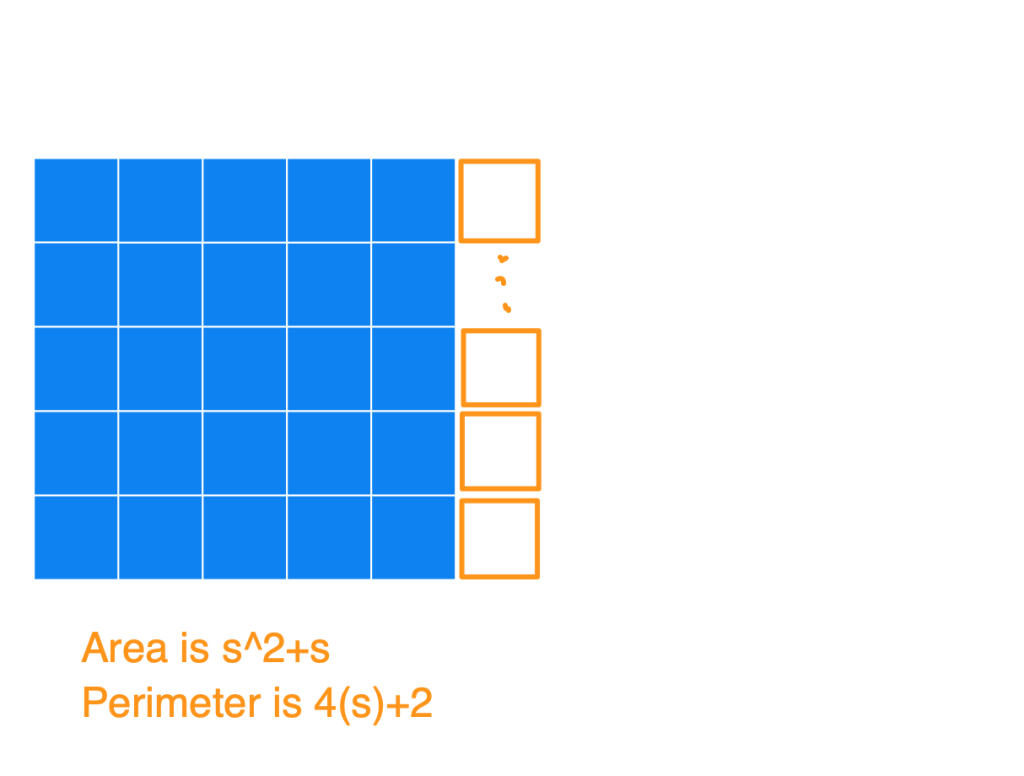
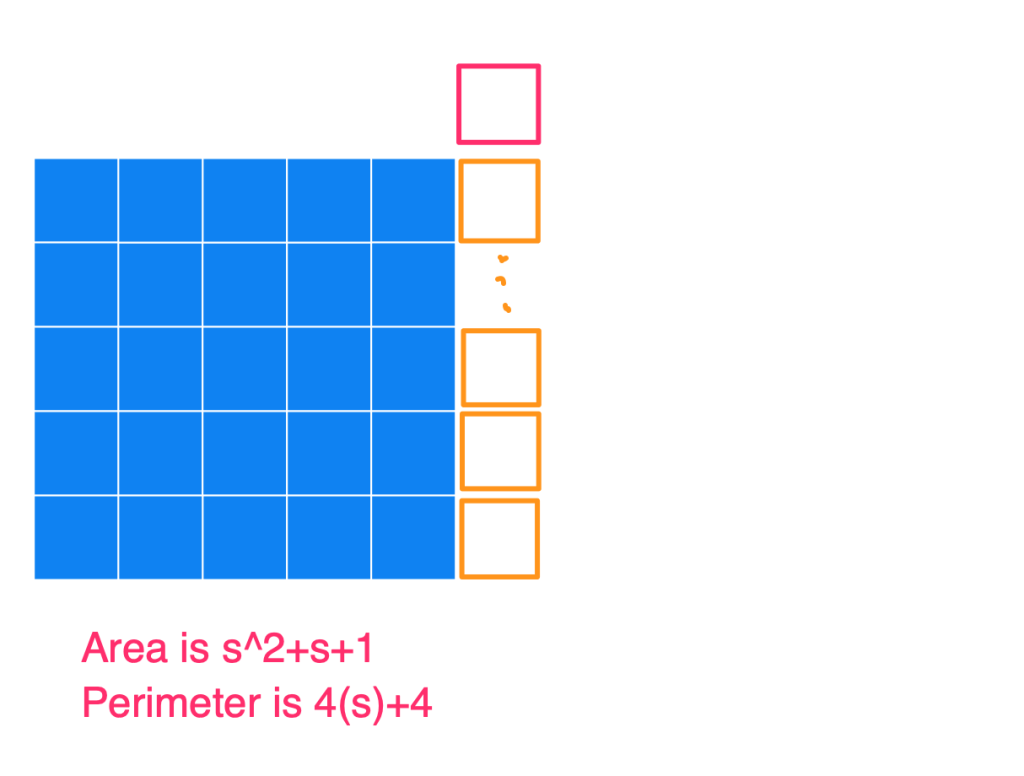
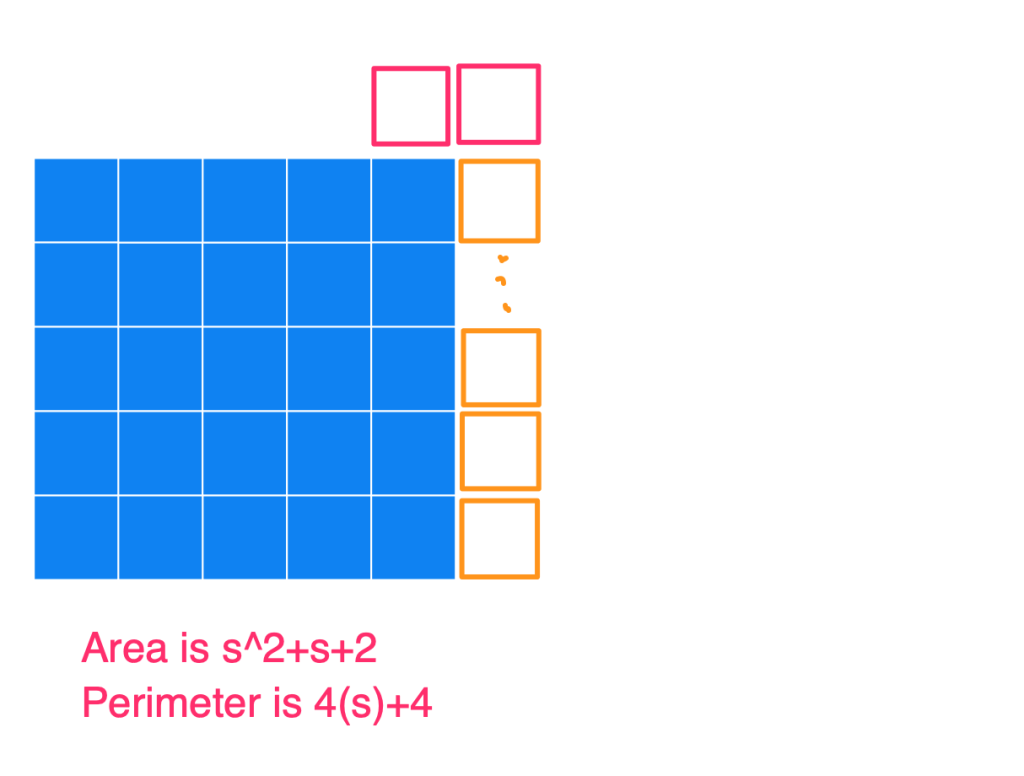
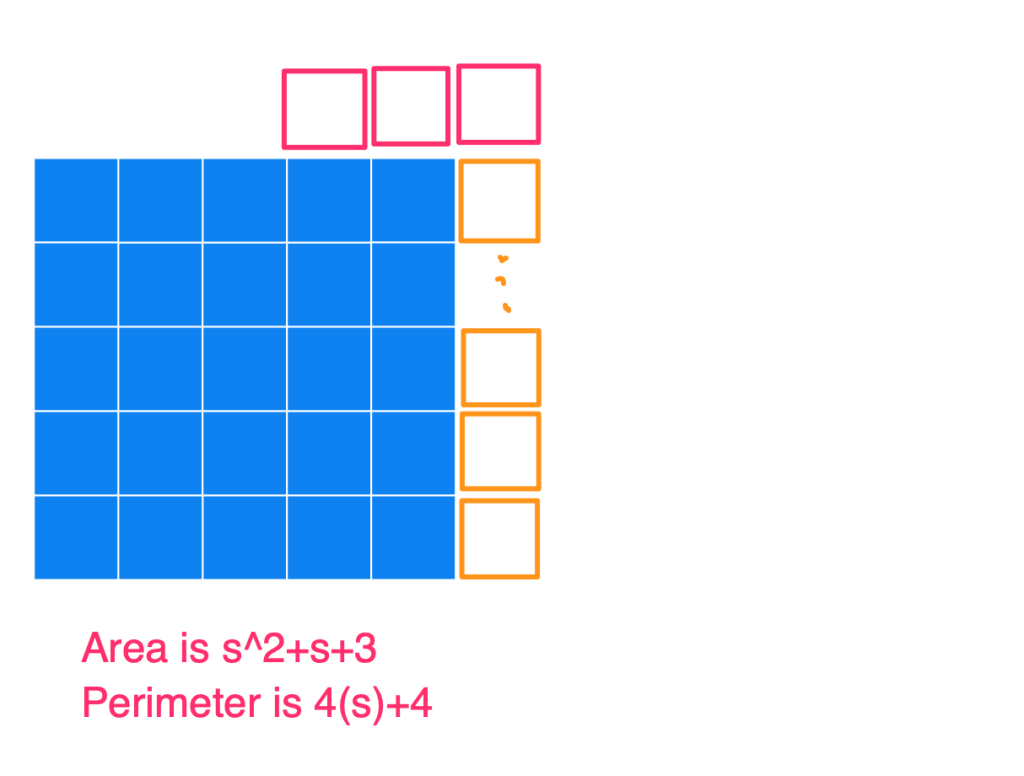
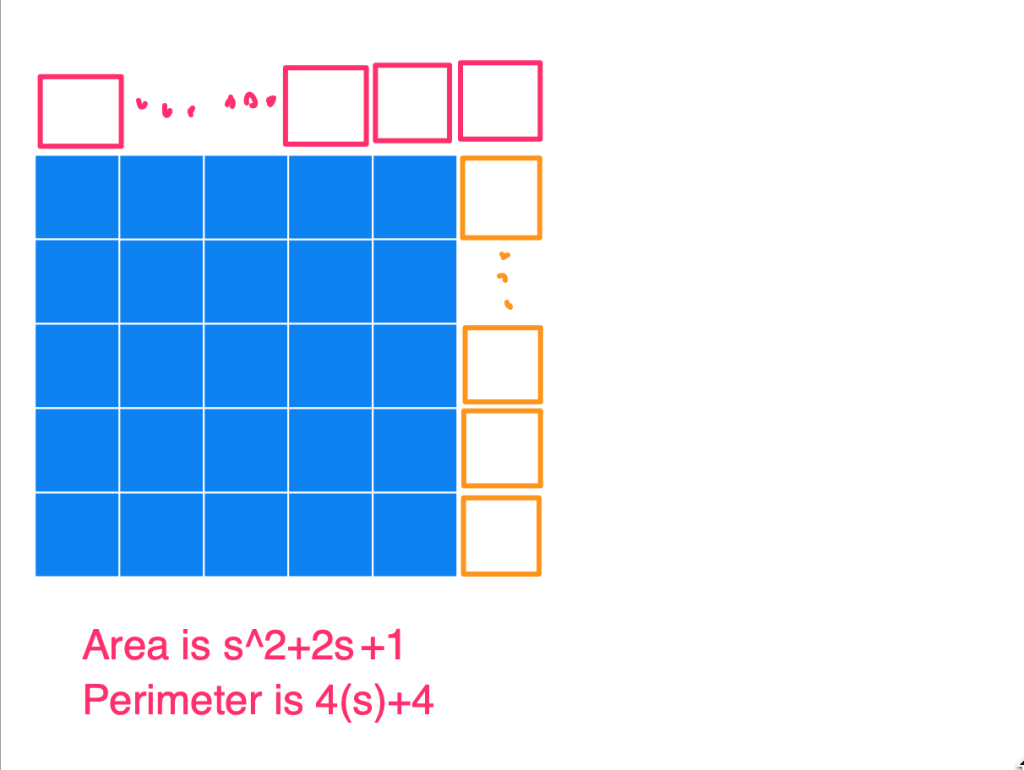
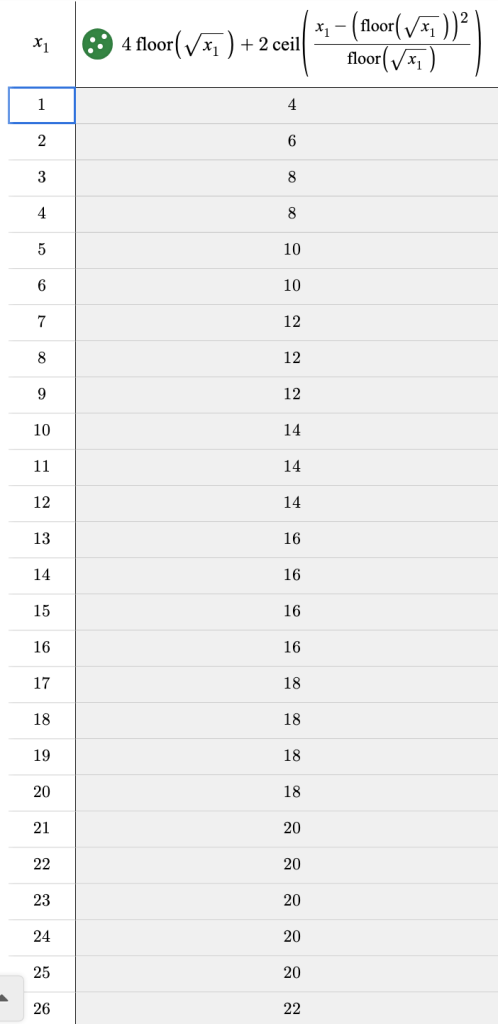
Basically, the way to construct the figure with a minimum perimeter is to create the largest square you can, and then append the remaining blocks to it. Below I have a series of images to show what the figures could look like for an Area of 25, 26, 27, …, 36, and also the Perimeters. I used s in the image (instead of 5) to show how this generalizes for any square number.

Some observations:

(1) Notice that after you start with that perfect blue square, each time you add a square (so for an area of s^2+[1, 2, 3, …, s]) you’ll always get the same perimeter of 4s+2. At this point, you’ll have an s by (s+1) rectangle.

And then when you continue on adding more squares to this rectangle (so for an area of s^2+[(s+1), (s+2), (s+3), … (2s+1)]), you’ll always get the same perimeter of 4s+4.

(2) At the end, when you’ve finished this process, you’ll have a new area of s^2+2s+1, which simplifies to (s+1)^2. And the perimeter of this is 4 times the side length of the square, which is now s+1. So this makes sense as 4s+4.

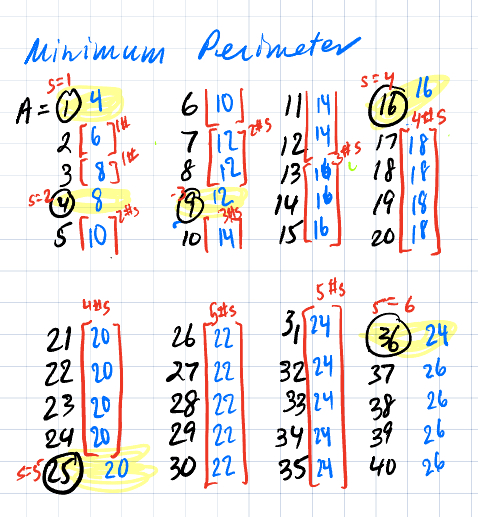
Here’s a chart I made which shows how the perimeter goes up after you hit perfect squares… Notice we know the perimeters of perfect squares, so for example at A=16 (a 4 by 4 square), the next four numbers will have a perimeter of 18 and the four numbers after that will have a perimeter of 20. That’s then when we hit the next perfect square of A=25.

So far, we have this:

Take your Area of n and find the largest perfect square the goes into it. Call that s.
If the remainder is 0, then you have a minimum perimeter of 4s+0.
If the remainder is 1, 2, 3, …, s, then you have a minimum perimeter of 4s+2.If the remainder is (s+1), (s+2), (s+3), …, (2s), then you have a minimum perimeter of 4s+4

However I didn’t want a formula in terms of s. I wanted an explicit and closed formula in terms of n. I wanted a direct answer to the question: if you have an Area of n, what is the Minimum Perimeter in terms of n? And I got it…

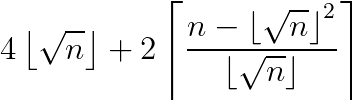
It’s kind of ugly looking, but hopefully you can see the motivation. The first part is just 4s. The second part is the correction factor (of +0, +2, or +4). The numerator in the ceiling function calculates the remainder. When you look at the entire ceiling function*2, it will give you 0 when you have a reminder of 0. It will give you 2 when you have a reminder of 1, 2, 3, … , s. And it will give you 4 when you have a remainder of (s+1), (s+2), (s+3), …, (2s). I was pretty proud when I was able to use my table above to figure this out. I checked using Desmos to confirm!

At this point, I’m confident about these bounds for the Perimeter of a figure with Area n…

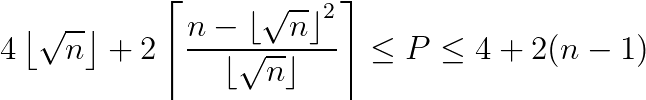
Now I’m stuck on the very last thing… I am confident with my formula for the Minimum Perimeter, but I haven’t proved it.

I think I have a way to show that if the Area is a perfect square (so n^2), then the Minimum Perimeter always occurs when the squares are arranged to form an n by n square. However at the moment I can’t seem to move forward from there.

In any case, that’s where I am with this problem!