A friend found this Sangaku, which if you don’t know (from Wikipedia) are Japanese geometrical problems or theorems on wooden tablets which were placed as offerings at Shinto shrines or Buddhist temples during the Edo period by members of all social classes.
So here’s what she sent me (from here)

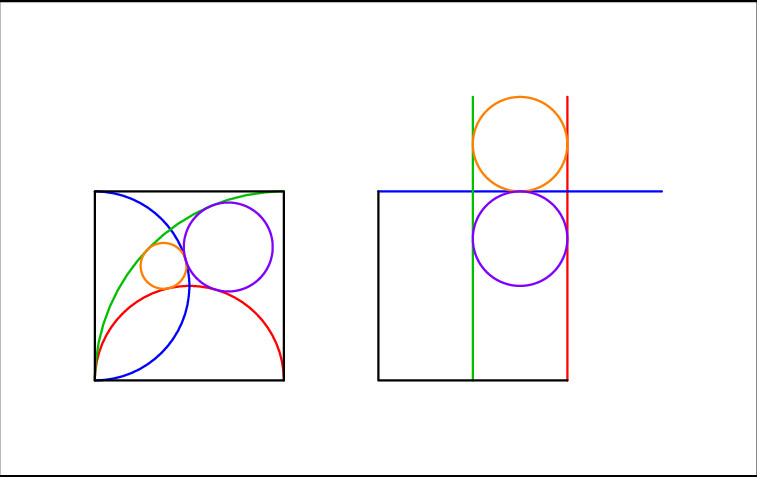
The question that I’m attempting to figure out is: what is the radius of the small circle in relation to the length of the side of the square? And you’ll see from the text she sent me, there is the answer.
We found the puzzle curious and we thought the figure was lovely, so we decided to make a piece of stained glass math-art for it. (We’re trying to teach ourselves how to make math-based stained glass art. As you can see from the picture below, we’re still very much novices!)

I spent over an hour on the problem this morning. I played on Geogebra to get the contours of the problem itself to help me understand the constraints. And then since I didn’t have a better approach, I started brute forcing it. I came up with equations when I put everything on the coordinate plane (using calculus to find slopes!), found some tangent lines, and looked for intersection points of these lines. I knew it wasn’t efficient, but I thought it would at least help me see how things would shake out I was hoping lots of terms would drop away…

Alas! The algebra got messy, and then I thought I’d have a system of equations that could be solved.

To be frank, I’m pretty sure in the mess of algebra, these equations are probably not correct. And I couldn’t really solve them anyway. (If you’re wondering what a, b, and c are, they stand in for slopes of the three lines (pink, light blue, green).
I’m officially annoyed and ready to give up. At least for now, or for a few days, or maybe forever. BUT the reason I’m posting this is that I’d really love a solution. Why is the radius of the circle 4/33s (where s is the side length of the square)? What is the approach to figuring this out?
So if you like geometry puzzles, like these Sangaku, or the puzzles of Catroina Agg (https://bsky.app/profile/catrionaagg.bsky.social), help me out!
UPDATE: I posted about this online and here are some of the assists I’ve gotten. I was going to look at them today but I’m not feeling super well.
From Facebook:
Bowen: “Check out Descartes’ Circle Theorem…” [here]
From Jason: “I am sitting across from Bowen this morning and UNBEKNOWNST TO ME, you sniped us both in parallel. Unbelievable. I solved it on paper, got all excited, and then saw that Bowen– SITTING ACROSS FROM ME– has already supplies that link above. Anyway, I’m not going to let him Liebniz my Newton here. I did some work on paper independent of him and will publish it with pictures in the comments below.
I went to https://en.wikipedia.org/wiki/Problem_of_Apollonius and used these equations:

The algebra I algebra’d.

I mean, I did not write the work in a way that was designed for other people to write, so there are a LOT of “S” letters that might either stand for “the numerical length of the side” or “the name of the solution circle”, depending on context.”
From BlueSky:
From diffgeom: If we invert the plane ((r,θ) -> (1/r,θ)) about the point where the three large circles meet, each maps to a coordinate line; the small circle maps to a circle whose center and radius look easy to find, and inverting again should give the radius?
Will give this a try…
I replied: Omg- my brain!!! Wow! I don’t know if I’ve ever inverted the plane and I didn’t even think to look at this problem through polar. I’m so intrigued!!! Essentially you’re saying the diagram will look easier once we do the inversion, we find the answer in the inverted world, then put it back?
diffgeom replied: Possibly a fun stop on your travels to learn about inversion: https://noai.duckduckgo.com/?t=h_&q=cylindrical+mirror+art&ia=web
[At this point, I looked up and watched this amazing 27-minute Numberphile video that explains some of the basics of inversion and got me excited: https://www.youtube.com/watch?v=sG_6nlMZ8f4]
tcorica replied: So, I’ve captured everything in a Desmos sheet EXCEPT how to take the final circle and un-invert it to find the uninverted center and radius. Any hints? I’m avoiding “reading up” on inversion, but I will if needed!
https://www.desmos.com/calculator/rzkrhnudqe
P.S. I flipped the image across the horizontal so that the given circles had centered on an axis, making it easier to write the polar equations in terms of r. @samjshah.bsky.social
tcorica also shared: I saw the responses suggesting “inversion” – i.e. recasting the problem by writing equations r= and then rewriting them as r’=1/r=. I’ve still managed to avoid looking inversion up 🙂, but I’ve done some thinking and experimenting with it – it’s a surprising and cool technique.
I’ve found a reasonably nice solution to this using inversion. Because the answer is a weird looking fraction, I’m wondering if perhaps there actually isn’t a pretty geometric solution to this pretty problem!
As an introductory exercise, I found it useful to consider the problem of finding the intersection of the circle with radius P and center at (P,0) with the circle of radius Q and center at (0,Q). E.g., show that the POI lies on y=(P/Q)x. Tons of approaches possible, inversion being one. 3/3
diffgeom replied: My approach: A circle of radius r at distance R from the center of inversion has points at distance R±r on a ray; inverting in the unit circle gives points at distance 1/(R±r), so the radius is (1/2)(1/(R-r)-1/(R+r)), or r/(R^2-r^2). (IIRC, the distance to the center is half the sum, R/(R^2-r^2).)
nsato7 also commented after diffgeom:
As @diffgeom.bsky.social points out, inversion takes care of the problem nicely. (And many of these Sangaku problems were solved by inversion.)
The three arcs invert to three lines. There are two circles that are tangent to these three lines; we want the “top” one.
mqb2766 shared: Similar to the other posts, a modern version of this problem is gps/trilateration with the distances from the known centers being 2-r and 1+/-r so 3 quadratics in 3 unknowns – the center and the radius. You get a trivial solution of r=0 as well as the stated one.
https://en.wikipedia.org/wiki/Trilateration
noswald also shared (unrelated to the others): My inelegant solution would be to impose a coordinate system on the figure and set up three equations involving the coordinates of the inscribed circle and its radius. We know the distance from the center of the circle to a corner is s-r, to one side’s midpoint is s/2-r, and to another side is s/2+r
From Email
My friend Japheth W sent me his written work, which he said I could archive here, noting “It’s not quite publication ready, but probably understandable to math teachers who are experts at reading even more disorganized student work.”
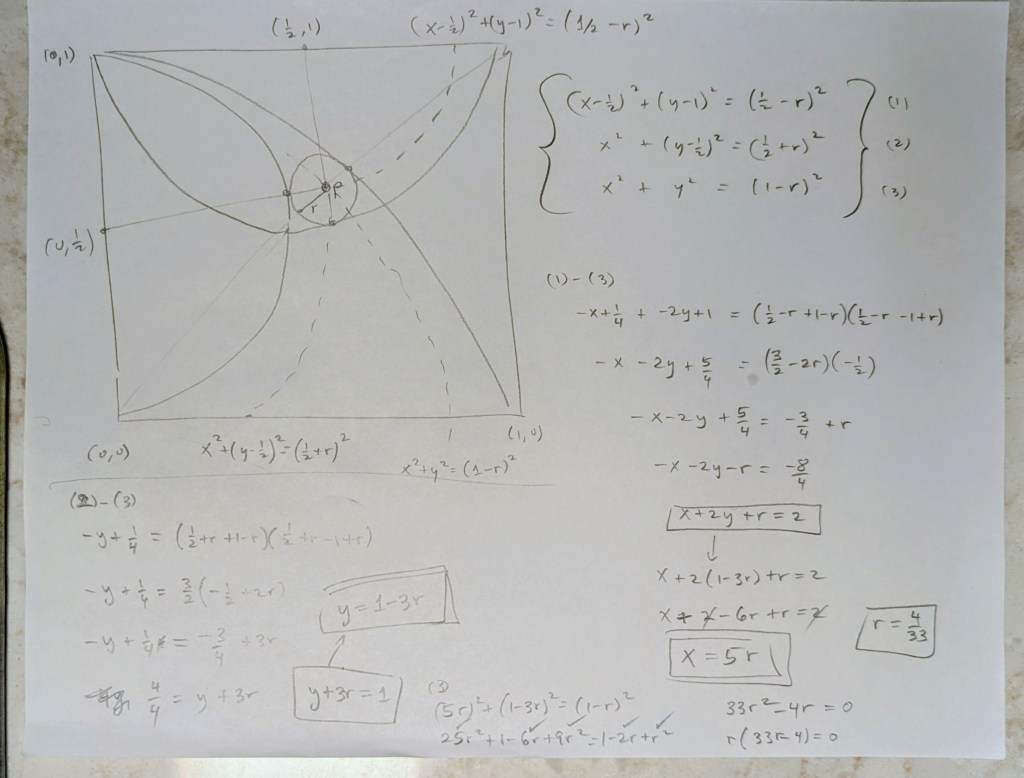
Sam, I found a solution, but it is still pretty messy and algebra heavy, so I wonder if there is a more elegant solution. I set the center of the small circle to be (h, k) and the radius to be r, with s as the side length of the square. Using the centers of the three larger circles, (0, s/2), (s/2, 0), and (s, 0), and their distances to (h, k), s/2 – r, s/2 +r, and s – r respectively, I set up three equations using the distance formula (squaring both sides for simplicity.) I knew with three equations and three unknowns I should be able to solve. With some algebra work I got to r = 1/5 k and h = 3/5 k, then substituted back into an original equation to get k = 20/33 s and thus r = 4/33 s. It was a little messy, and I can send you a .pdf of my work if you email me at krees@ma.org. Maybe I’ll clean it up later today.
Kevin
Thank you! I’m so glad you shared this. I’m putting this away for a while since I’m not feeling well but I definitely email you if I need. Thank you for the offer to send along your work! I also shared an approach that others were suggesting (“inversion”) above when I updated this post a few minutes ago. (I didn’t want to lose all the help I got!). Thank you again!
It seemed to me pretty simple, since the tangents match on the circles, the radii must line up, so the there are three equations for the center of the circle:
x^2+(y-1/2)^2=(1/2-r)^2
(x-1/2)^2+y^2 = (1/2+r)^2
(x-1)^2+(y-1)^2 = (1-r)^2
Solving that system with Wulfrom alpha for a positive r gives
x = 1/17 (6 – sqrt(2))
y = 1/17 (4 + 5 sqrt(2))
r = 1/17 (3 sqrt(2) – 1)
Note that I did not get r=4/33, so it is quite possible I made an error.
Found my mistake. I made a sign error.
I reparameterized to put the origin at the center of thebig circle:
solve x^2+y^2=(1-r)^2, (x+1)^2+(y-1/2)^2=(1/2-r)^2, (x+1/2)^2+(y)^2=(1/2+r)^2 for x,y,r
gives two solutions:
(-1,0) r=0
(-7/11, 20/33) r= 4/33
Based on the condition of two tangent circles, their point of tangency must lie along the line connecting the centers of the two circles. Upon drawing the diagram, it becomes apparent that the three lines are strongly related to both the side length of the square and the radius of the smaller circle. These three lines intersect at the center of the small circle.
Let’s set the bottom-left corner of the square as the origin. The center of the small circle has coordinates (x,y), the side length of the square is s, and the radius of the small circle is r. Using the Pythagorean theorem, we can derive the following three equations:
x^2+ (y – s/2)^2 = (s/2 – r)^2 ——————-(1)
(s/2 – x)^2 + y^2 = (s/2 + r)^2 ——————-(2)
(s – x)^2 + y^2 = (s – r)^2 ——————-(3)
By subtracting equation (2) from equation (3), we obtain: x=3r
Next, subtract equation (1) from equation (2) to get: y=2r+x=5r
(Just a side note: I think this coordinate is really cool!)
Finally, substitute this (3r, 5r) into any of the equations (e.g., equation (1)), and we get: r=4s/33
By the way, the stained glass piece turned out really beautiful!
It seems my sketch didn’t upload properly, so here’s the link to the image: https://imgur.com/a/rlSEX4p.
Let O be the center of the circle, let A be center of left semi-circle, let B be the center of the bottom semi-circle and C be the bottom-right vertex of the square.
Consider Triangle AOB:
AO = s/2-r
OB = s/2+r
AB = s/ rt(2)
Consider Triangle OBC:
OB = s/2+r
OC = s-r
BC = s/2
Applying cosine rule:
OC^2 = OB^2 +BC^2 – 2*OB*BC*Cos (angle OBC)
AO^2 = AB^2 + OB^2 – 2*AB*OB*Cos (angle ABO)
Angle OBC + Angle ABO + 45 = 180
Angle OBC = 135 – Angle ABO
Cos (Angle OBC) = Cos (135-Angle ABO) = Sin ABO/rt(2) – Cos ABO/rt(2)
rt(2) Cos (OBC) = Sin (ABO) – Cos (ABO)
Solving cosine equations gives:
Cos OBC =(6r-s)/(s+2r)
Cos ABO = (s+4r)/(rt(2)*(s+2r))
Sin ABO = rt (1-cos^2(ABO)) = rt (s^2-8*r^2)/(rt(2)*(s+2r))
Substituting and solving, r = (4/33)*s