Ages ago, I kickstarted the “hypnograph” which is a cycloid drawing machine.

I tried to get it to work when it arrived, but for some reason, I couldn’t get the drawings to work out. (The instructions that it came with were okay but there were bits that could have been much clearer.) However I found this box in my closet a few days ago, and decided to try again. And it worked!

Here are some drawings I’ve created:

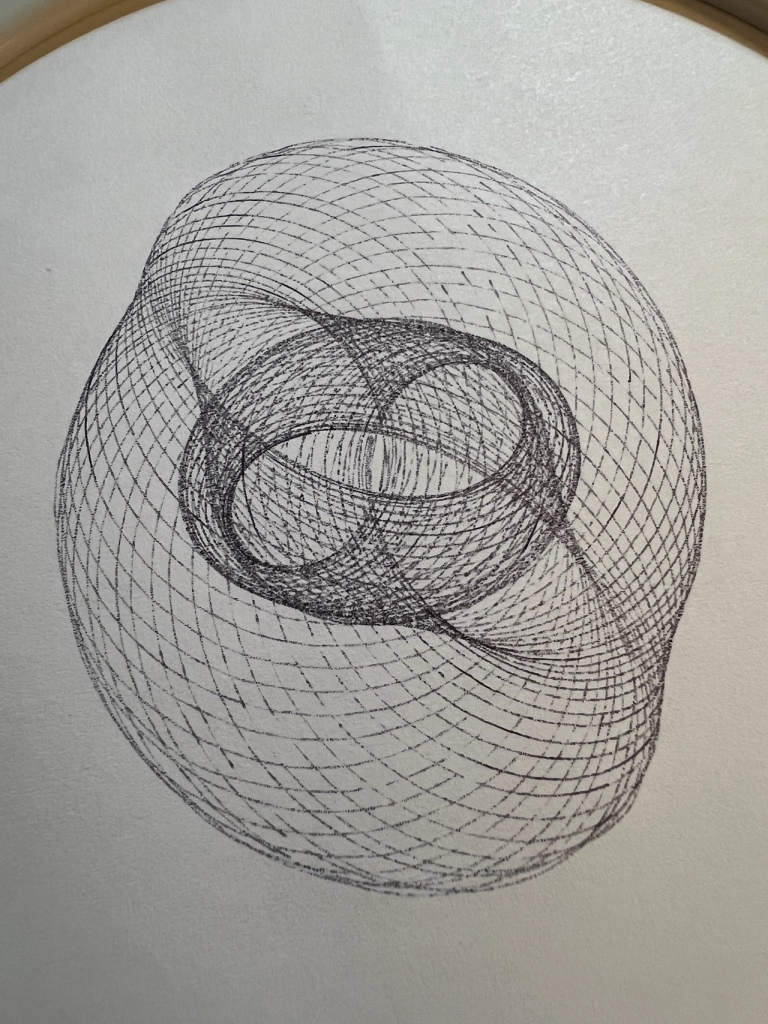
You can see the machine in action in this youtube video [starting at time 4:53]:

Of course I wanted to somehow mathify this. In fact, I’ve never even mathified sprigraph before (though I’ve seen some people derive the equations, but I’ve never tried to do it on my own)! I decided to jump right in and see: can I come up with equations for the final graph, given all the components of the machine?

It was harder than expected, and I had moments of frustration and felt like I wanted to quick. It took me a couple days. I first started doing all this algebra on paper, and realized that was not going to work because the equations got gross. So instead, I went to Desmos and everything became much easier.

Without going into too many details, here’s my setup in Desmos, and a picture of the hypnograph, so you can see the connections:

I have point B spinning around a circle/gear (and you can change the location, the rate of rotation, and size of the circle/gear), Similarly I have point P spinning around a second circle/gear (with the same things changeable). The arm that connects B and P is fixed at point B, and slides at point P (like with the machine). (I’d watch the video above to see the difference between the fixed point and the sliding point. In that video, the fixed point is on the red gear and the sliding point is on the green gear.)

Initially, I had Desmos plot just the pen location. It was creating some really pretty drawings, but it didn’t mimic what I saw on the hypnograph itself. The hypnograph images always have some sort of symmetry, and my final result didn’t always have that symmetry.

I posted my Desmos and a video of the machine working on Bluesky to see what I was missing. I knew I just needed fresh eyes to show me what I was blind to. And diffgeom clocked it (and dandersod agreed)!

Not sure this is the only issue (and have not checked your model), but the paper is rotating relative to the table (and therefore relative to the rods holding the pen), while on your screen it appears not to be…?

YEESH! I forgot to have the paper rotate as the pen was drawing! ACK! But thinking about that hurt my brain. I came up with one solution, and tried to implement it, and that failed. But with some perseverance, I came up with a solution and I think it works! [1]

Here’s an image from my Desmos sheet to show you what it produced:

And if you want to play with the Desmos sheet, change the gear sizes, the length of the two arms, and the speed of the gears and rotating paper to see the various results, here you go! Click on the random image below I made in Canva, and press play. It’ll look like garbage at first as it’s drawing and then suddenly you’ll see how cool it looks!

Now I should qualify to say I’m not 100% sure this is perfectly correct. But I wanted to share what I had because I’m proud of it. And it was fun! And if I don’t write it down, I’ll never have a record of working on this project!

Archiving for later: These youtube videos [one, two] are great for getting a sense of the machine and how to modify it so it works the best.

[1] A bit of an aside/archive that won’t make sense to anyone not in my head: Essentially I realized I was doing a hack for polar coordinates but not allowing r to be 0. So it was graphing the right equations but having all negative r graph as positive r. When I realized that, I finally figured out what I needed to do. I made the center of the spinning paper (0,0). That had to be fixed. Then I had the coordinates for the pen. So I put those coordinates through a rotation.

The pen location was at this point:

So to make the equivalent marking on a moving paper, I multiplied it by the rotation matrix (where the rotation matrix was filled with values that had the wheel rotate at a certain rate):

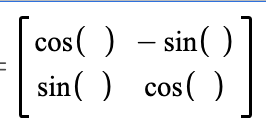
Which got me the pen location after it had been rotated! In my Desmos page, that turns out to be:

Honestly I was really proud of this solution! And what I love about all this work is it incorporates all the stuffI teach in precalculus… polar coordinates and rotation matrices FTW! We stopped teaching much about vectors, but I used a bunch of vector thinking in this also!