Calculus

My 2009-2010 Course Expectations

Below are working drafts of my course expectations for next year. Most things — in terms of wording and text — haven’t changed, although the grading breakdowns have. In case it wasn’t glaringly obvious, I’m all about having super clear expectations for my students. Anyway, you can see that aspect of my teaching come through in these.

Algebra II Course Expectations, 2009-2010

Calculus, Course Expectations, 2009-2010

Multivariable Calculus, Course Expectations, 2009-2010

Feel free to steal anything, if you like anything.

A Clock, Speedometer, and Odometer walk into …

At the beginning of the summer, I went to a conference at Exeter, and vowed to blog about some of the things I learned from it. Which I haven’t made good on, yet. There were a few gems, and I thought I’d write about ’em briefly in a series on mini-posts.

The first is a simple way to get kids to think about the meaning of a derivative or an integral conceptually, before they’ve formally been introduced to it. It’s a Gedankenexperiment (thought experiment) and the presenter said they actually do it on parent visitation day, so the parents can think too.

You’re in a car with three things: a speedometer, an odometer, and a clock. Everything is going along dandy, until suddenly, your speedometer breaks. Can you tell how fast you’re going? You don’t want to get pulled over by the cops, after all.

That’s it. Can you imagine how fun that conversation would be to listen to, as a proverbial teacher-fly on the wall? And then to get to lead that discussion? Obviously, most students are going to talk about the problem as if you are going at a constant speed. Getting them out of that mindset will be awesome.

Of course, the natural second question is what happens if not the speedometer, but the odometer, breaks. Can you tell how far you’ve gone?

I dig this thought experiment. I mean, it’s so simple I don’t know why I hadn’t thought of doing it to motivate our work. Heck, you can have students talk in groups and present their ideas. Good stuff.

A Great Calculus Problem… that is Powerfully Related to Geometry

I’m sitting in a building at Exeter, digesting lunch and waiting for the next session to begin. I’m at what has so far been a really valuable math teacher conference. What impresses me most, besides the amazing and neverending supply of food that they offer, is the population of teachers that come. Many of the teachers I’m talking with have 20+ years of experience in the classroom.

Over the next few days I’m going to use this blog to talk about some of the tidbits of interesting problems I’ve been presented with, to good resources or programs that I was introduced to, to neat ways to present topics in class, to ideas that I’ve been inspired to think about.

I’m going to start with a nice calculus problem — probably good for a AP Calculus BC class, but there is definitely a way I could show this problem to my non-AP class.

Here’s the problem. You’re in a museum and you’re looking at a painting which is hung above eye level. (There is a specific painting which is hung high in the entrance room at the Brooklyn Museum that I think of with this problem.) You are standing some distance away from it. The question is: what is the largest angle ( $\alpha$ ) that you can get as you walk forwards and backwards? (See diagram below for setup.)

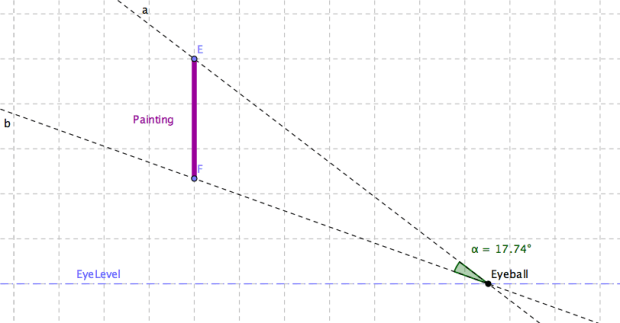
So to be clear, as you move the eyeball forward and backwards along the dashed blue line, what’s the largest angle you can create? Of course if you walk right up to the painting, or far away, the angle is going to decrease to 0. If you can’t see that, look at the diagrams below.

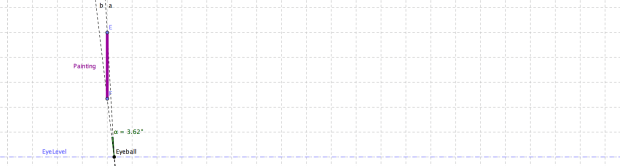
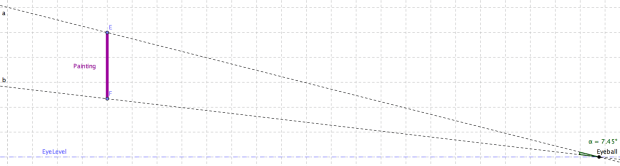
So of course there has to be some perfect distance that will give you the maximal angle. You see where this is going…

Find that maximum angle! (Use the variables in the diagram below.)

Of course this doesn’t have to be a painting. It could be, as the speaker pointed out, an overhead view of a hockey rink, with the painting being the goal, and the eyeball being the player with a puck. Where does the hockey player have the maximum angle to shoot and make it into the goal?

I want you to have the fun of solving it, but the solution I came up with was:

$\alpha=\tan^{-1}(\frac{P}{2\sqrt{Y(P+Y)}})$

(I can help you with that if you want. Just throw your questions or cry for help in the comments.)

However, there is something pretty amazing about this problem, something that is powerfully seen with geometry software like geogebra or geometer’s sketchpad. Check out the sheet I made and see what happens as I bring the person close to the picture and look for the optimal angle? When you look at this, try to see if there is a geometry connection to our solution for the largest angle…

Vodpod videos no longer available.

more about “Geogebra_Picture_Problem“, posted with vodpod

Do you see the geometry connection? The optimal angle exists when the circle created by the top of the picture, the bottom of the picture, and the eyeball is tangent to the line of sight. Now my charge to you — which would be my charge to my students — is to (a) explain in words why this is true and (b) use geometry to calculate this optimal angle. You know, this work is an exercise for the reader. I mean, I’m not going to do everything for you. Sheesh.

Student Reflections on Calculus

Nearing the end of the school year, but when things are still in full swing, I ask students to write a letter to themselves… to themselves at the beginning of the year. The letter should outline things that they learned about the class, about me, about whatever in hindsight that would be helpful for them to know to be successful in calculus class. [1]

I promised them — crossed my heart, hope to die, and all that — that I wouldn’t look at them until after final grades were in, so they should be SUPER honest.

What I get from these letters is not only insights into my students, but more than anything else, deep insight into me as a teacher. It also reveals a lot to me about my about students. Without further ado, here are the relevant excerpts [2] of each of these letters which I’ll be handing out on the first day of class next year. (And before you ask, some of the things in these letters are inside jokes between the class and me.)

View this document on Scribd

[1] At the beginning of this year, I handed out excerpts from the previous class’s letters.

[2] I pretty much included everything relevant… the good, the bad, and the ugly… the stuff I cut out either identified the student or were fluffy sentences that had already been captured.

My favorite book title

Here’s my favorite book title, ever. I always loved the power of the academic colon.

For more information on the author, Wikipedia has some details. (As an aside, if I had stayed in grad school, Silvanus was going to make an appearance in my dissertation.)

But the title is just the tip of the super awesome iceberg. You can read it on Scribd, but some of my favorite part so far is:

Prologue: Considering how many fools can calculate, it is surprising that it should be thought either a difficult or tedious task for any other fool to learn how to master the same tricks. Some calculus-tricks are quite easy. Some are enormously difficult. The fools who write the textbooks of advanced mathematics–and they are mostly clever fools–seldom take the trouble to show you how easy the calculations are. On the contrary, they seem to desire to impress you with their tremendous cleverness by going about it in the most difficult way.

And the first chapter is just two pages. Awesome.

This struck me especially deeply because… well, see some twitter posts I made earlier this week (read it from the bottom upwards):

After this brief burst of histrionics, I actually did decide that I wanted to change things a lot. In a follow up fit, I whipped up an email to my department head, pretty much begging that she would support my plea for a grant to work on revamping the curriculum in the summer.

(Turns out that revamping the calculus curriculum isn’t an immediate priority, sigh, so I will probably not get it.)

In any case, now that you’ve gone through this stream of consciousness, look back at my favorite book title and see how it all comes full circle.

Take what you don’t know…

In Calculus, I sound like a broken record. Each time we learn something new, I say “take what you don’t know and turn it into what you do know.” I say that at least three times a week. I said it last week when doing integrals like:

$\int \frac{1}{4x^2+1} dx$

We don’t know how to deal with that, but we do know how to deal with

$\int \frac{1}{x^2+1}dx$

So let’s try to turn what we don’t know how to do into something we do know how to do. For those who haven’t taken calculus for a while, the integral above is $\tan^{-1}(x)+C$ . So to do the original problem, we want to somehow get the original integral to look like $\int \frac{1}{(something)^2+1}d(something)$ — the integral of 1 over something squared plus 1. So we rewrite the integral as $\int \frac{1}{(2x)^2+1}dx$ . That’s much closer to what we want to get — it looks more like something we know how to deal with. Next we use $u$ -substitution to finish this beast off ( $u=2x$ ) to get $\frac{1}{2} \int \frac{1}{u^2+1}du$ . Now we have something we know how to deal with, from something we didn’t.

Again today, I showed my students how to solve $\int_0^1 \sqrt{1-x^2}dx$ , and told them to solve: $\int_0^1 5-3\sqrt{1-x^2}dx$ . At first sight, they recoiled, but again, we used the mantra of “take what you don’t know and turn it into what you do know” to solve it. If it looks scary, fine, have a moment of panic, but then ask yourself “what does this look like” and “can I turn it into that with some simple manipulation”?

I was thinking today how this actually could be my refrain in Algebra II also. Example: I could frame quadratics in that way. Students know — or quickly learn — how to solve equations like $(x+1)^2=5$ (hopefully). But what about something like $x^2+6x+1=0$ ? It’s not nearly as easy. But then we can talk about if there is a way to that what we don’t know (that equation) and turn it into something we do know how to solve ( $(x+3)^2=8$ ). It’s not that I don’t do this already, but I am not always explicit about it. It is not my mantra.

But it should be. It’s how we solve math problems. We have something we don’t initially know how to do. And we have to figure out if we can simplify/rewrite/re-envision it to bring it to a place where we know how to do it.It seems stupid and simple and obvious, so much so, that I don’t say all the time. But if I started saying that as my refrain, if students really saw that math is simply this simple process, it might stop seeming like a huge bag of tricks that never fall together. They might see it as the art that it is — where there is creativity in deciding how to get from point A (hard problem) to point B (simple problem they know how to do). And all the specifics that we do in class are giving them the tools which they can use to chisel out a path from A to B. It might finally be us always trying to work out the puzzle: what does this look like that we know how to do, and can we get it to that place?

In other words, we’re now talking processes instead of methods. We’re talking problem solving instead of rote memorization. And whenever a student is stumped on a problem, you can stimulate his/her thought process by saying “we’ve always taken what we don’t know how to do and turned it into something we do know how to do… what similar things does this beast remind you of?”

So yeah, it’s not a huge revelation or anything. But I’m thinking that it might be a really amazing experiment to frame my Algebra II and Calculus classes with this mantra next year. Heck, maybe even in the next few weeks when I’m teaching exponential and logarithmic functions! I mean, yeah $\log(2x+1)+\log(x-1)=2$ may look ugly. But is there a way to turn it into something we do know how to do? Namely something of the form $\log(something)=2$ ? Obvi.

Be careful what you plot

Today in Calculus, I was waxing euphoric about why what we’re about to embark upon is amazing — how we’re eventually going to be able to find volumes and surface areas of strange figures. Not your standard spheres or cylinders or cones, but strange, exotic figures.

So I decide to open WinPlot and produce a surface created by revolving around the x-axis.

As I pressed “Enter” to generate the graph, I immediately recognized that we were going to have a problem. But it was too late.

I could have picked any number of other functions, but I decided to pick $\sin x$ . Great.

We all had a laugh. Ah, high schoolers.

Moral: Be careful what you plot in class.

Continuous Everywhere but Differentiable Nowhere

I have no idea why I picked this blog name, but there's no turning back now