My favorite* online math puzzle contest — Monday Math Madness — has decided to use a problem that I submitted for a previous contest.

CHECK IT OUT HERE!

*It’s really the only one that I know. But that shouldn’t be taken disparagingly; the problems are just hard enough that you have to make one really rewarding conceptual leap, and just easy enough that with enough perseverance you know you can conquer it.

dy/dan has done something spectacular:

posted every single one of his geometry keynote presentations for the year.

I don’t teach geometry (and I’m glad because I never really liked it), but now I kind of wish I did have a section.

I’m inspired enough to say that one of my goals for the year is to do the same for my SmartBoard lessons with either Algebra II or Calculus. There aren’t a lot of Smartboards out there. Nor good sites for resources. But looking at this project from a microlevel, instead of the macrolevel, it isn’t so daunting. Maybe I’ll try to post my SmartBoard lessons each week somewhere.

Wow! I am totally on a blog posting roll. I think the end of the summer has me going out less, which has me putzing around the apartment more, which has me thinking about school and math more. (It doesn’t help that I don’t really get reception on my TV and I don’t have cable.)

In any case, MathTeacherMambo pointed me to this (warning: VERY ADDICTIVE) game:

BLOXORZ

For those who are starting their pre-start-of-classes meetings, I warn you that you might not ever make it to those meetings. Your principal will knock on your door, but you’ll be drooling and staring vacantly at your computer screen, cursing the day you ever reached level 11, 12, or n.

For those who are wisely taking my advice and holding off playing the game, here are a few examples:

As you can see, the goal is to get the block in the hole.

I think this is a great open math problem ready to be attacked and solved by a high school student. Fundamentally, I think with a lot of work, a student should be able to answer the following question:

Given a particular floorplan and starting block position, can you decide whether the floorplan is solvable? Can you tell, without playing the game, whether there is a way to get the block in the hole? 

To illustrate, two simple examples of floorplans — the first one is obviously not solvable, the second one obviously is.

What about this third one?

The first two are easy to solve by inspection. Even the plan above is easy to solve by inspection — but you’ll notice it gets slightly harder. I want to know — even in the most crazy floorplan — is there a solution? If not, I want proof that there is no solution.

The game itself has a bunch of complicating elements — like transporters, and ways to get more floor to appear by having the block roll over a button. (See the second video above.) But I think the base case is hard enough — with none of that nonsense.

Once the initial problem has been solved, I think a great follow up question would be: what is the fewest number of moves you can solve a particular floorplan in? 

I have a student who approached me about doing an independent study of linear algebra or differential equations this year. I know I’m going to be overwhelmed, so I had to decline. However, I suggested that instead of having a formal course, we could work on an investigative problem together. I just emailed him this idea — but I don’t know if he’ll want to.

PS. I’m guessing a good starting place for this problem is looking at the work that has been done on the Lights Out game. (I’ve never played it, but it seems like it’s similar enough in nature that that solution can inform our approach.)

The Water Cube in Beijing — you know, the one where swimming god Michael Phelps just broke all those world records? — has been touted in the media for being a very green building, capturing over 90% of the solar energy that hits it. However, in addition to looking cool, did you know that there is some incredibly deep mathematics behind the structure itself?

Lord Kelvin (William Thomson) was a prodigious and prolific nineteenth century thinker, and one of his interests was studying bubbles. (Seriously.) But to preface this post, take a moment and think about a single bubble. Why does it form a sphere — and not a cube or blob shape? The answer deals with forces and energy and the like, but the problem reduces to finding the figure with the smallest surface area for the amount of air contained in the bubble.

And if there are two bubbles touching, we know they meet and form a dyad of bubbles. And three bubbles meet, and they will always meet at 120 degrees. And more?

The more the bubbles, the more they are touched on different sides by other bubbles, forming flat faces. We end up seeing that the bubbles form polyhedra!

What if you had a whole bunch of bubbles in a foam bath? What would be the idea formation of them?

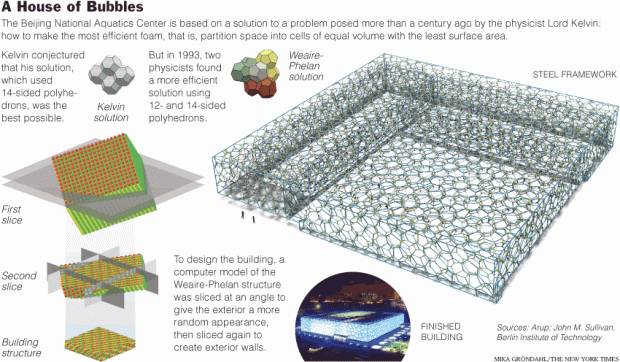
In 1887 Lord Kelvin asked the question: what is the shape that partitions space in such a way that the shape has the minimum surface area?

One example of a shape that partitions space would be boxes — stacking boxes, one on top of each other, in all directions. But boxes end up not having minimum surface area. Spheres aren’t a possible answer, because you can’t fill space with spheres — there will always be gaps between the spheres!

Bubbles, by their very nature, partition space by taking the shape that minimizes surface area. Kelvin studied bubbles and conjectured that the answer to his question was “tetrakaidecahedra.” Well, in his words, “a plane-faced isotropic tetrakaidecahedron.” (These are truncated octahedra.)

And in fact, there is a slight curvature, but “no shading could show satisfactorily the delicate curvature of the hexagonal faces.” But no worries, because you can see them yourself, like Kelvin did, by making a physical model:

it is shown beautifully, and illustrated in great perfection, by making a skeleton model of 36 wire arcs for the 36 edges of the complete figure, and dipping it in soap solution to fill the faces with film, which is easily done for all the faces but one. The curvature of the hexagonal film on the two sides of the plane of its six long diagonals is beautifully shown by reflected light.

I find it extraordinarily awesome that even though you can work on mathematics with pen and paper, you can play around and experiment with soap bubbles to see solutions.

It turns out that Kelvin’s conjecture was wrong. It wasn’t until 1993 that it was shown there was a better shape. Denis Weaire and Robert Phelan found shape that had 0.3% less surface area than Kelvin’s shape. To do this, they had to use a computer program!

Their shape was more complicated looking. (Kelvin’s shape was formed from a single cell; Weaire and Phelan’s shape was formed from two different types of cells.)

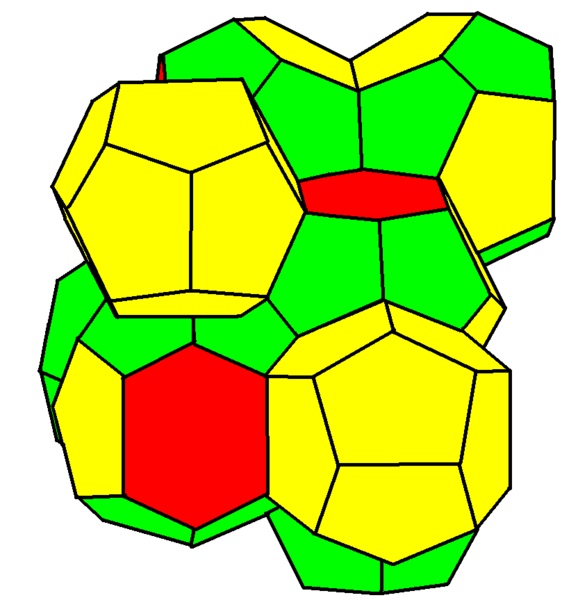
If you want to build your own, you can print out the nets to fold here!

Wikipedia states:

The Weaire-Phelan structure uses two kinds of cells of equal volume; an irregular pentagonal dodecahedron and a tetrakaidecahedron with 2 hexagons and 12 pentagons, again with slightly curved faces…. It has not been proved that the Weaire-Phelan structure is optimal, but it is generally believed to be likely: the Kelvin problem is still open, but the Weaire-Phelan structure is conjectured to be the solution.

And this structure was the inspiration (and formed the basis) for the Water Cube in Beijing; we’ve come full circle. Surprising is the totally random look to the structure (like it had no order behind it). That was an effect achieved by taking a cube composed of the Weaire-Phelan structure, and then slicing it not horizontally, but at a 60 degree angle. See the excellent NYT graphics below.

I tried to make up my own problem along the lines of this problem, but wanting it to be slightly different.

Let . Show that exactly.

Coming up with your own problems is so much harder than solving problems.

(If you need help, see the solution to the problem linked above. The general method I used for solving this problem is the same method I used for creating this problem.)

I was browsing old math journals a few days ago and got caught up in looking at puzzles/challenging problems sent in by professors to The Mathematical Gazette (the original publication of the Mathematical Association).

I got engaged in battle with a problem from it’s first year of publication (No. 1, Vol. 7, April 1896 – if you have JSTOR access, see the original problem here). The journal stated that it was a question “from recent Entrance Scholarship papers at Oxford and Cambridge.”

I think it’s a darn good problem, so take a stab at it. I’ll type my solution to it below the fold, but maybe you’ll get a better one? (I went down two wrong roads before I came up with this one…)

(more…)