We left off in our quest for an explicit formula for the nth Fibonacci number having created this amazing generating function:  .
.
To do what we’re about to do, I need to remind you of two precalculus things:
First, that  . If you don’t know why, I suggest doing long division!
. If you don’t know why, I suggest doing long division!
Second, partial fractions.
I’m going to go through this explanation assuming you know these two things.
So let’s look at the denominator of our 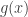 and factor it. Okay, okay, you got me. There isn’t a nice factoring with integers. But it can still be factored, of course.
and factor it. Okay, okay, you got me. There isn’t a nice factoring with integers. But it can still be factored, of course.
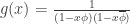 , where
, where 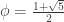 and
and  . Using partial fractions, we get:
. Using partial fractions, we get:

We’ve made good headway, but what we don’t know are  and
and  ! However, noticing that we can use the first precalculus topic above, that
! However, noticing that we can use the first precalculus topic above, that
 .
.
Rewriting this as a simple polynomial, we get:
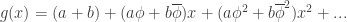
Now we’re almost done! We use the initial conditions to find out  and
and  .
.
Since we know  and
and 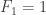 , we can say
, we can say 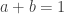 and
and 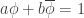 . Solving these two equations simultaneously yields
. Solving these two equations simultaneously yields 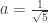 and
and 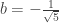 .
.
So the nth Fibonacci number is: 
which simplifies to:  .
.
Which is what we set out to show! Huzzah! What’s also nice about this (besides the fact that it’s an integer, which is surprising) is that it shows that the Fibonacci sequence grows exponentially!
one. (I had to do that… I started teaching probability to my seventh graders and we reviewed factorial today.)
