Month: July 2008

MIT, I’m disappointed in you

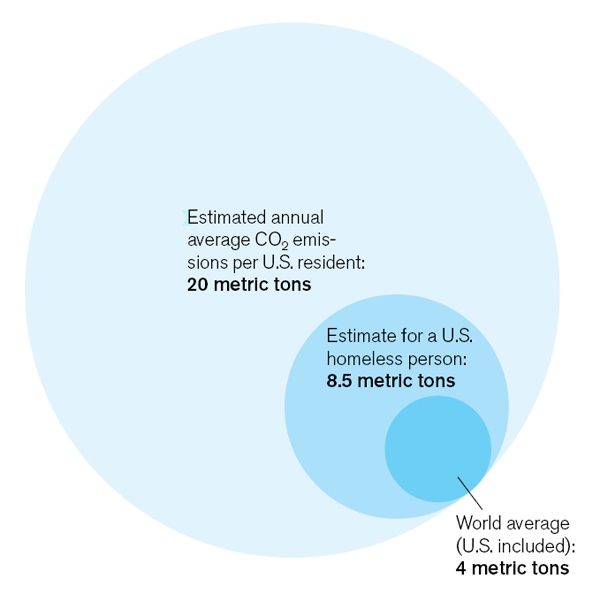
I love the MIT magazine Technology Review. This month’s issue had the following diagram in it, associated with an article about carbon footprints:

Anyone else see the problem? And anyone else see a teachable moment?

If you don’t see it, think about the data. You’re saying the World Average is 4 metric tons, the US Homeless Person is 8.5 metric tons, and US Resident is 20 metric tons. In any representation of the data, the US Homeless Person should be a bit less than twice the World Average. And the US Resident should be five times the world average.

Now look at the picture. Does that diagram represent that?

Put it another way: can you fit exactly five of the small circles in the largest circle?

(No.)

The diagram is misleading because you look at it and naturally compare areas. But unless you give it more than a glance, you won’t notice that the numbers (4.5, 8, 20) actually are the radii of the circles!

This could be the hook for a geometry or Algebra I class (on proportions, on circles, on data analysis). A teacher could then to parlay it to a discussion of how to “fix” the problem…

I see two easy solutions:

  1. Make a bar graph (boring solution)
  2. Make the same bubble graph, but make the radii \sqrt{4.5}, \sqrt{8}, and \sqrt{20} respectively (more fun solution)

In coming up with the second solution, students will think about areas, proportions, and visual representations of data. I can see students each approaching and solving the problem slightly differently, but still getting the same answer. In that sense, it allows for some grappling and struggle.

I still love the Technology Review. Not only is it full of good reads, but good ideas for lessons!

Look below the jump for a revised graph, which accurately represents the data…

(more…)

A challenge for my students; or, laying down the gauntlet

This is too good not to use in the classroom… mwa hahahaha.  (Found via Digg: here)

A simplistic explanation (which is all I wanted) is here:

Your brain can make your hand write a 6 in the normal direction no problem at all, and it can circle your foot in a clockwise direction, no problem at all either. But when you try to do both types of movement at the same time, big problems.

This is because your brain now has to send very different movement instructions to your arm and leg together at the same time. Your brain is simply not used to doing different things with your arm and leg at the same time in this way.

Note: another one is to “try to simultaneously rotate the index fingers of both hands in the same direction (clockwise or anticlockwise). Do it slowly at first, then faster, and faster…. Pretty soon, they’re going in opposite directions.” (from metafilter)

Math History on the Net

arXiv.org was originally designed to be a repository for pre-prints of physics articles, but it has since been expanded to other disciplines. I recently discovered that even though most of the math pre-prints are out of my league, there is one category of math articles that I have a good chance of understand: math history.

So if you want to explore mathematicians writing the history of mathematics, go here. (I found an interesting article on the solution of the Poincare conjecture in this haystack.)

The former historian in me has to point out, however, that for the most part, mathematicians writing history (of mathematics) is fascinating for the general “we are interested in math” audience. But historians will cringe at the teleology and absence of any culture in these narratives; they tend to be self-contained, internalist, and lack nearly everything that historians value in their craft.

There are really good historical works on mathematics written by mathematicians, I’m sure. But I guess I want to say that there are really good historical works on mathematics written by historians too. I would argue — from what little I’ve read in both realms — that these works by historians are often better, more considered, and more interesting. And the really good ones don’t skimp on the mathematics either, but delve deep into the mathematics, and relate the mathematics to culture.

A few from the top of my head:

Karl Pearson: The Scientific Life in the Statistical Age (Ted Porter)
Masters of Theory: Cambridge and the Rise of Mathematical Physics (Andrew Warwick)
Mechanizing Proof: Computing, Risk, and Trust (Donald MacKenzie)*
*Actually, this is a sociology of mathematics book.

Help? Multivariable Calculus!

I need help! GACK!

So I’ve decided that my one week of lazing about and reading (finished Middlesex and the teen novel It’s Kind of A Funny Story, and started Heat) is officially over [1]. It’s time to get to work!

A mere two hours ago, I hoisted the Multivariable Calc book that I’ll be teaching from next year from the pile on the floor to my desk and gave it my first run through. It looks okay [2].

I’m designing this course from scratch, and I wanted to ask for some advice for anyone who has taught it, or has ever designed a course from scratch…

  1. Anything — print or web resources, jokes, songs, videos, pictures? Also, it doesn’t have to be about multivariable calculus; any advice on how to design a really awesome course from scratch would be much appreciated! How long did it take you, what resources did you draw upon, did you make a general outline of topics or a specific day-by-day schedule, did you write your assessments beforehand or during the school year once you’ve gauged the students’ abilities, and the other million questions that I’m thinking of.
  2. Does you know of any good software for graphing in 3-D that is open source (read: free) and works on a PC? I know of SAGE, and OCTAVE, and the like, but I’m wondering if those programs are a bit overkill for this course. Is there something less bulky out there? Maybe even a really powerful 3-D graphing calculator that people like? 

    UPDATE: I just remembered that SAGE came out with the online SAGE notebook, which is what I think I’ll probably implement! It’s like MAPLE in terms of the command line, and it seems extraordinarily powerful. 
     

  3. How do you teach your students to graph in 3-D by hand? How do you do it on the board? SmartBoard?
     
  4. Have you ever taught a class with 3-5 students before? Do you treat it like a regular class — with lecturing but with more individualized attention? Or did you teach it seminar style? What would a seminar style math class look like?
     
  5. Do you have any good investigative activities or projects for multivariable calc? Or that you do in calc that can be extended?
  6. Have you ever just thrown out teaching from a textbook and used an online textbook? Or mixed and matched textbooks? Or taught without any book?
My big idea at the moment is to make a course with no exams. These are kids who are accelerated enough to have taken AP Calculus before their senior year. I want to expose them to the idea that math can be a big series of puzzles. That math can be investigative instead of regurgitative. That math can be collaborative. That math can be hard and challenging and rewarding if they persevere. And since we have a tiny class (maybe 3-5 students), this is definitely possible. So as I said, no exams. Instead, we’ll have nightly homework assignments with the more fundamental and basic questions, and then “problem sets” with investigative problems due at the end of each chapter. The problem sets can be worked on alone or with others, but the write-ups need to be done alone, and they will be graded on correctness and clarity. Who knows, maybe I’ll even teach them to use LaTeX (well, MiKTeX) to write up their solutions.

Hopefully I’ll use this blog to post about the evolution of the course design as the summer progresses… so don’t change that RSS reader!

[1] Other books that are lined up to be read this summer are Fight Club, The Kite Runner, and The Adventures of Huckleberry Finn (all for school); if I have time, I also want to read Lazarus’ Closed Chambers, Tartt’s The Little Friend, Dewey’s The School and Society and The Child and the Curriculum, Pais’ The Science and the Life of Albert Einstein, and finish up the second half of Gogol’s Dead Souls. 

[2] I’m using Anton’s Calculus, Early Transcendentals, 8th Edition. My school uses the first half of the book in calc classes and I don’t want to make my students buy a second book. My initial opinion: the book is okay but seems to be unnecessarily dense in places, and could have left a number of sections out. The exercises at the end of each section are quite good.

Delicious Linky Links

I’ve been doing a lot of “internetsing” in the past few weeks. Some things of note:

  1. Math Teacher Mambo’s “volumes of revolutions” project [here]
  2. A superduper awesome puzzle to give to your students when learning trigonometry: “explain this crop circle” [here]. If I gave extra credit, I would probably give it to the student who could explain the math encoded within it.
  3. Wordle [here] creates clouds from texts — text frequency. I love the idea for using this to create images for a English class website (different word clouds, different books), or for the cover of a dissertation or a book. I created the images below. Guess which books they are for? (I got them from Project Gutenberg.) An interesting English discussion could spring out of this type of word counting…
  4. SensibleUnits.com [here] converts standard distances and sizes to things we non computers understand.Example: 500 gigabytes is 17 dual layer HD DVDs, 160 Human Genomes, 62 Window Vistas Installation, 190 English Wikipedias (without images)
  5. For an English or History class, have students design a facebook page for famous authors, poets, scientists, political figures, etc. Look at this one for Einstein on DaleBasler.com [here].
More to come. Later.