I was browsing old math journals a few days ago and got caught up in looking at puzzles/challenging problems sent in by professors to The Mathematical Gazette (the original publication of the Mathematical Association).
I got engaged in battle with a problem from it’s first year of publication (No. 1, Vol. 7, April 1896 – if you have JSTOR access, see the original problem here). The journal stated that it was a question “from recent Entrance Scholarship papers at Oxford and Cambridge.”
I think it’s a darn good problem, so take a stab at it. I’ll type my solution to it below the fold, but maybe you’ll get a better one? (I went down two wrong roads before I came up with this one…)
SOLUTION
Let . Keep in mind that’s what we’re trying to find. If we calculate
we get something nice:
Rearranging, we get
.
But recall we are given . Simplifying the right hand side of the equation above, we find it equals the very pretty
. (Do you see how? Remember to rationalize the denominator of
.)
Oh! So now we know
. Clearly we know
must be of the form
to yield this answer. So we calculate:
Expanding out, we get
Equating the left hand side and right hand side, we see that
[Eqn 1] and
[Eqn 2].
Let’s factor out an from Eqn 1:
.
Since I’m lazy, let’s first investigate the easy case, if . (If it doesn’t help us, we’ll then consider the other possibility.) If
, and plugging that into Eqn 2, we get
.
This actually can be factored! (If you can’t see that, graph it and find that a nice root is 4.) It factors into:
.
The only real root is (The quadratic yields imaginary roots.) So in fact we don’t need to deal with the other gross zero of Eqn 1 because we have a workable solution. (Phew. Factoring that cubic was hard enough.) We have now found that
and
and we’re done. We have solved for
which was our goal:
An interesting side note is that no one solved and sent in their solution for this problem in time. I searched through a number of subsequent issues to see if there was a published solution, to see if it differed from my own, but I found the journal’s policy:
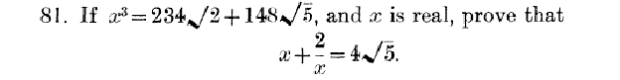
I got up to u^3 – 6u = 296rad5, but then I got stuck. I didn’t see the insight to substitute a + brad5. I have this inability when a solution is available to not peek. Even though it takes all the fun out of it. Nice problem, thanks for sharing.
Haha, I too am afflicted with this peeping tom disorder. Maybe we should call it “Peeping Pythagoras Disorder” or something cheesy.
However I am still pleased with myself for not looking at the solution to the following problem (from a recent IMO) while I let my subconscious brain mull over it:
Show if you know
if you know  and all three variables are nonzero.
and all three variables are nonzero.
But I’m so frustrated that I might let the disorder take over!
I might be missing something here, but…If I solve the 2nd equation as a simple quadratic, and then cube my solution, and come up with x^3 equals 234*sqr(2)+148*sqr(5), doesn’t that complete the proof? It appears that this only solves the converse of the problem, however, I will have demonstrated that the cube root of 234*sqr(2)+148*sqr(5) indeed satisfies the required 2nd equation.
That seems too easy, but…???
No no, you’re totally right! I I’m pretty sure that’s what I first did. But I think I wanted the challenge of going in the forward direction. Because if the problem asked you to find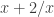 in simplest form, you wouldn’t be able to use your method.
in simplest form, you wouldn’t be able to use your method.
But I definitely don’t see anything suspect with your method.