We are now delving into some interesting coordinate geometry. We’re also beginning to use patty paper. And today the other geometry teacher and I had an awesomely fun conversation that revoles around something you might find it fun to think about.
Here’s the impetus/setup.
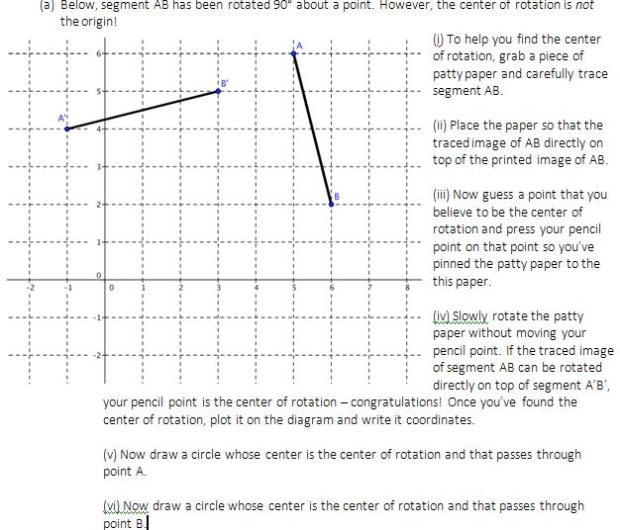
We have just finished talking about translations, and we’re moving on to reflections and rotations. When we introduce rotations to kids, we give them a backwards problem pretty early on: here is a figure and here is the rotation of the figure. Try to find the center of rotation. Use patty paper and guess and check.
This is an awesome exercise (inmyhumbleopinion) because it has kids use patty paper, it has them kinesthetically see the rotation, and it gives them immediate feedback on whether the point they thought was the center of rotation truly is the center of rotation. Simple, sweet, forces some thought.
This is our intro. We have a few more exercises in our problem packet similar to this. But then we move on. Le sigh. This felt wholly unsatisfying to us, because at its heart we left our kids hanging. We never get at the obvious question. How do I find the center of rotation without guessing and checking.
How do we take this introduction and make it mathematics?
The Challenge
[Baby challenge: Figure out how to find the center of rotation, given any figure and a rotated figure. This is not totally simple, okay? I’m calling it a baby challenge only because the next challenge is sooooo hard!]
Imagine you’re a geometry teacher, and you want students to discover a “foolproof method” to coming up with the center of rotation (given an original figure and a rotated figure). You also want students to be able to understand (deeply) and articulate why this method gives you the center of rotation.
What do you do to achieve these twin goals?
(This is what the other teacher and I were discussing today, and having loads of fun doing it!)
You don’t need to answer this question in the comments. (Though you’re welcome to throw down any ideas.) I’m actually not looking for advice. (We’re well on our way to coming up with an answer to this.) I just thought it would be a fun thought exercise for you, if you like thinking of lesson planning/curriculum design. This is the type of stuff I love thinking about — when I have time!
This is backwards planning at it’s most fun, in my opinion. I have a deep result that is abstract and hard to grasp. I have very concrete 9th graders who I want to get from knowing almost nothing to discovering, understanding, and marveling at this great mathematical insight. How do I get from Point A to Point B?

My first thought is “Get rid of the graph paper”.
Then you could nudge them into seeing what happens to a single point under rotation.
Then to take any two points and think about a rotation that takes the first to the second – oops, there’s lots of them !
Nearly there now !!!
With a bit of luck they will see that the 90 degree angle is a red herring.
Construct perpendicular bisectors of corresponding points. They’ll have to intersect at the center of rotation.
I know the “how” (using a different method than gasstation), but I’ve never really stopped to consider the “why”. Thanks for the poke to do so!
I’d recommend a paper without grid, with pre-image & rotated image already on it, vertices labeled.
Lessons are always done in context, so maybe you want to have given the kids a reflections lesson on finding the mirror line before this, talking about the perpendicular bisector as a mathematical tool to find the mirror line.
Ask, is the distance from A to A’ the same as from B to B’ ?
Ask, which of our mathematical tools could we try?
I’d love to follow this general process: observations –> hypothesis –> testing hypothesis –> connection to previous knowledge to help kids prove/justify their hypothesis. Did you guys succeed in helping kids discover the method?
Not as formally as you wrote, but I think we’re doing a version of it. We highlight the idea of play –> conjecture (induction). But then from conjecture, we talk about figuring out ways (sometimes multiple ways) to deductively figure stuff out.
For this particular post, what we ended up doing is https://samjshah.com/2014/10/26/a-follow-up-regarding-centers-of-rotation/