I have all the feels, coming back from #TMC16, but they also have paralyzed me. There’s a disconnect between all the feels, my making sense of all the feels, and my ability to express all the feels in words. I felt paralyzed because I wanted to express things right. Since that was impossible, I did nothing. But to get past that, and because I need to collate the gems and thoughts from the conference to learn from them, this post is going to be a random collection of thoughts. It’s more for me — to consolidate my thinking and write down all the little things — so apologies if it feels like a confusing brain dump.

What are you passionate about? 

Sara VanDerWerf (her blog) gave a keynote that was reminiscent of a keynote last year. She said “What are you an evangelist for?” (For her, one of those things is Desmos, because of the equity and access it allows her kids.) Once you know that thing — the thing you are willing to go to bat for, the thing you want to spread — you should think consciously about how to best evangelize it. That might include having an elevator speech ready for you to give, and being conscious of the different audiences you may be talking with about it (students? parents? teachers? admin?). Being an evangelist isn’t just being passionate… it includes enacting that passion by finding ways to share “the best… with others who can benefit.”

Sara’s fabulous calculator museum (mausoleum!)… all your calculators are dead… all hail Desmos!

I know I am an evangelist for the #MTBoS. However in terms of math content or math teaching, I don’t quite know what I’m an evangelist for… yet. All this reminds me the end of this blogpost I wrote last year after TMC, where I was trying to figure out what my “brand” was (and came up emptyhanded). But I have faith that with enough time, I’ll figure it out.

Speaking of evangilism… Jonathan Claydon (his blog) shared a “my favorite” about Varsity Math, a community he’s built up at his school. I’ve had a teacher crush on this guy for years. There’s something about his energy and style and humor, and the fact that he is good at something I am not (yet) good at (being a “relational” teacher)… he’s a must follow. In any case, Jonathan is an evangelist for changing the way kids look at math at his school. Although ostensibly his goal is to increase the numbers of kids taking AP math classes and increase the AP scores of these students, he’s doing it by building a supportive math community — one that feels like a club. He is doing this by creating “shared experiences.” He knows he has succeeded if he can get kids to say “I love (varsity math). (Varsity math) feels like family. You couldn’t understand because you’re not in (varsity math).” The only way the last statement could make sense is if an entire culture is built around (varsity math). Of course what goes in the parentheses is open. Read about his project here. See a photo of @rawrdimus here:

This “my favorite” spoke to me. I’ve been consciously working at my school about raising the math department. Not in terms of teaching and learning (I don’t have much say in that), but in terms of getting kids engaging with math outside of the math classroom. I brought the New York Math League contest to school, I’ve worked (with another teacher) to concertedly increase the number of students taking the American Math Competition each year (from around a dozen to seventy+). I found a non-stressful virtual math team competition that students can compete in so that they can fit it in their busy schedules. I have co-advised math club for years. I started Intersections with a science teacher, a math-science journal for students to submit their works to (it’s now four years old!). Lots of things… I want spaces and times for students to engage in math outside of the classroom. But with all of this, I don’t see a culture of kids who geek out about math. There isn’t a community or culture around doing mathematics at my school. And Jonathan’s talk helped me realize that I have to think intentionally about building a community. It is more than “if you create it, they will come.” It isn’t the event or space that I design, but the “shared experience.” What does this mean? What does this look like? I don’t know yet. But perhaps having a student-created chant before each virtual math team competition, bonding field trips (math movies? museum of math? math scavenger hunt?), swag as proud identifiers, a wall of fame…

[Update: I was having trouble figuring out what precisely I want to accomplish in my school. And today is day 3 of a crazy math frenzy day where I’m having fun exploring and writing lesson plans and playing around and coding and getting stuck and getting unstuck and having frustration and elation — so much elation. And then I read this post by Annie Perkins, which talks about a sort-of-crisis I’m having (posts here and here). And in my current haze, I see the glimpses of what I want to achieve. Why do I want kids to engage with math outside of the classroom? Because it’s beautiful and fun to play with and just play mind-blowing cool. But they don’t get that in the classroom — at least not regularly enough. Jonathan created a community of kids who were vested in AP math. I think I want to figure out how to create a community of kids that love to (a) be exposed to interesting/strange things about math, and (b) play with math and explore it. Less “math team tricks” and “competition problem solving strategies” and more pure unadulterated fun. Things like this fold and cut problem that I did in geometry. Or generating and analyzing their own fractals. Taxicab geometry. And I think lecture might be okay for some of this — a lecture on infinity or Godel’s incompleteness theorem. Or following some internet instructions on how to build a planimeter out of a sodacan to calculate the area of a blob just by tracing around it. Or going as a group to a math lecture at the Museum of Math. Or learning about higher dimensions. Whatever! I want to get kids to geek out about how cool and fun math can be. I want a math is cool community, where there is a culture of nerd-sniping and geeking out and regular mind-blowing-ness. The truth is I probably don’t have time this year to come up with a plan to execute this to make it happen this year. I also think that the lack of free time that kids have in their schedules might make any plan of mine totally impossible. But I think it’s worth brainstorming… maybe not for this year… maybe for next year.]

Desmos Features:

At the Desmos preconference, I learned about three things

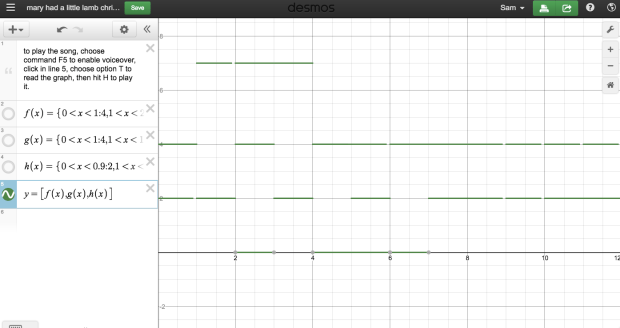
(1) “Listening to graphs.” This feature was included for vision impaired students, but I think many of us teachers started dreaming up other uses for it. To get a sense of it, check out this piece (done by Rachel Kernodle and James Cleveland) playing “Mary Had A Little Lamb” (click on image):

 

To play (at least on a mac), press COMMAND F5 (which enables voiceover), go to the fifth line and press OPTION T (to tell the computer to “read” the graph with sound), and then press H (to play the graph). When it’s done, you can turn off voiceover by pressing COMMAND F5 again.

Some thoughts… Have the audio for some periodic and non periodic functions, and have kids do an audio function sort? Play audio of graphs (without telling kids that) and have kids do a notice/wonder (before sharing what they are listening to). Have kids identify if a graph has a horizontal asymptote for end behavior from an audio file? Have kids identify which graphs might have a vertical asymptote from an audiofile?  Play sine and cosine (or secant and cosecant) and have kids not be able to tell which is which (because they are just horizontal shifts of each other). Have kids devise their own piecewise functions and play them, while other kids have to graph them. Create a piecewise function and have a student who enjoys singing to sing it? I am not convinced that anything I’ve thought up could help a deeper understanding of any topic, but I also don’t think it could hurt. Some kids might really get into it and enjoy playing with math…

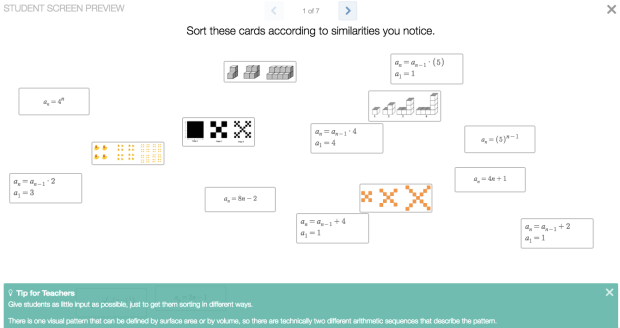
(2) Card Sort: You can create card sorts in desmos now! Check a bunch of them out (that were created at the Desmos pre-conference)! Or if you just want to go to one of them, click on the image of Mattie Baker’s card sort on visual sequences:

To gain this functionality on your desmos account, go to teacher.desmos.com and click on your name in the upper right hand corner, click on LABS, and then turn on Card Sort.

(3) Marbleslides: You can create your own marbleslides in desmos also! Turn it on in labs (see above). Then you have the capability of building your own! If you don’t know about marbleslides, check out this marbleslides activity made by the desmos folk on periodics.  At least to me, the use of marbleslides is to help students understand function transformations… so I can see it useful for helping kids gain fluency in transformations. (Anyone see another use for marbleslides, that I’m missing?)

Showing Student Work

Hedge talked about how she uses SnagIt to display student work. She takes a photo of student work on her phone, and using an app called FUSE, transfers it to SnagIt (on the laptop) — as long as both are on the same wifi network. Here’s her blogpost showing it in action! It costs money ($29.95) but I trust Hedge!

I attended PCMI years ago, and I recall Bowen and Darryl using this technique (kids working on problems, taking pictures of different approaches) to facilitate discussion to bring different ideas together. Nearing the end of a session, they would project pictures of student work, people would explain their thinking. Bowen and Darryl would sequence the pictures in a thoughtful way. They wouldn’t focus on those who “got the answer” but on various approaches (visual/algebraic) — whether they worked to get the answer or not. I liked that so much, and I suspect SnagIt could allow that to work for me in that way.

Getting Triggy With It! Hands On Trigonometry

 

Fouss gave a wonderful hour long session on making trigonometry hands-on for students. Instead of telling us what she did, we got to do some of the activities, and that was powerful. There were activities I’ve read about that I thought “eh, okay, but it would be more efficient to do X, Y, and Z” and then I did them and I saw how the act of doing them could be helpful. Here are three that we got to do: understanding radians with smarties, creating a unit circle with patty paper, and creating a trig wheel to help kids practice converting between radians and degrees and visualize what the size of the angles look like.

All her materials are linked to from her presentation, and are easily found on this folder on her google drive. I have to scour them to find my favorites. I did love the radian activity. If you make the radius of the unit circle 7 smarties long, then you can have a good discussion on whether 3 radians is 180 degrees or not… (21 smarties won’t quite make it to 180 degrees… but 22 smarties will fit snugly… nicely giving the 22/7 approximation for . Nice!)

Some of the ideas linked to from her presentations that I want to steal:
(a) Trig Stations
(b) Two Truths and a Lie (useful for more than just trig!)
(c) #TrigIs (useful for more than just trig!)
(d) If I choose to do ferris wheel problems, this ferris wheel comparison [but modified to be more challenging]
(e) Desmos’s Polygraph for Sinusoids and Marbleslides for Periodic Functions
(f) If I teach trig identities, use this matching game (and have kids check their answers once they are done by graphing on desmos!)
(g) Headbandz, trig edition! (for graphing trig functions)

Variable Analysis Game

Joel Bezaire presented a great game that can be used in warmups to help students see relationships and patterns. His video on it is here, showing the game and how it is played:

Nominations: Making Work Public

Kathryn Belmont (@iisanumber) gave a great way to have kids really put forth effort on open-ended assignments without using grades as a stick. She will ask kids to do this assignments, and then put their work on their desks. Each student gets posts its, and as they wander around the room, they put post-its on the works they see… They write two accolades for good things, and two ways to push back or improve the assignment. The way I envision this in my classroom, not everyone will see everyone else’s work, but everyone will see 5-6 other students’s work. After the walk about, the teacher says: “Do you have any nominations”? Jake might reply “I would like to nominate Kiara.” If Kiara feels okay about being nominated and “accepts the nomination,” the teacher takes Kiara’s work and puts it under the document camera. Then Jake might say, “Kiara did … and what I thought was so awesome about it was …”

(Her slides for her mini-talk are here. A video of her talk is here.)

The teacher is no longer the sole audience member for the work, and kids are defining what good work looks like. In Kathryn’s classroom, she saw a huge increase in kids putting in effort in these open-ended assignments. (I can see this being useful in my own class, especially when I do my explore math mini-explorations.)

Intentional Talk 

I went to a session by Jessica Breur (@BreurBreur) which was fantastic. Although it was only one hour, I wish it were a morning session. She wants to have teachers establish a culture where students:

• use the group to move the group forward
• talk, trust, and depend on classmates and the teacher
• persist — even in the face of a challenge
• view math as “figure-out-able” and accessible to all

She highly recommended Cohen’s Designing Groupwork (a book which I have but haven’t read).

To start, over the first week or two, students will be doing lots of groupwork activities. And at the end of them, they will (in their smaller groups) focus on what the group “looks like” “sounds like” and “feels like.” They don’t necessarily need to focus on all three at once — students could focus on “sounds like” during one activity and “feels like” on another. After the week is done, the class comes up with a set of norms in these three categories — where they talk about what successful/good/fun groups look/sound/feel like.

We did a lot of hands-on work trying out some of these groupwork activities — and she has included all of those activities in her slides. Here is one of my favorites:

This is the red solo cup challenge. A group of 3 or 4 is given 6 red solo cups, stacked inside each other, placed face up on the table (so like a regular drinking up face up). The students are given a rubber band with four strings tied to it (even if 3 students are doing this, keep the four strings). Student must put the solo cups in a pyramid formation. If they finish that, there are other configurations that Jessica includes in her presentations (or students can design their own challenge for others!). Afterwards, the group reflects.

Similar tasks can be done, like 100 Numbers, Saving Sam, Four 4s [but making an emphasis that we want as many ways to generate the numbers 1-20, not just one for each], Master Designer, or Draw My Picture.

For more “math-y” things, you can do a Chalk Talk/Graffiti Board– where students answer questions before a unit to activate some old ideas. For example, “What do you know about the number zero?” [In fact, any sort of talking point/debate-y statement can be used here.] Kids write anything and everything they know on a poster in their group of four. Then hand the posters up and students walk around and read other students’ responses (if time, writing their own comments down). Finally, for closure, you can ask students aloud or using exit slips “What are two things you didn’t think about that you saw on the graffiti boards?” Another more math-y thing is a donut percent task. An example is here but I’m confident it could be modified for trigonometry (values of trig functions, identities, etc.) or rational functions (equations and graphs) or any number of things! The idea behinds this is that each person in the group is given four slips of paper, and as a group, four complete donuts have to be created.

Sounds simple? But here’s the rub… group members must follow the rules below to each get their own donut completed.

You should keep a poster of the 8 Standards of Mathematical Practice, and every so often during activities or groupwork, ask students which ones they are using.

Once norms are established at the start of the year, you consciously need to be doing activities that practice the norms. Be intentional about it. (If you find that kids aren’t listening to each other, find an activity that promotes listening.)

I loved this session. However what I need now are a set of activity structures that I can fit actual mathematical work into. So things which develop understanding, or practice solving something, etc. And it would be nice not only to have the activity structures, but the activities themselves all in one place (so, for example, activities for Precalculus!).

Talk in the Math Classroom

My morning session was called “Talk Less, Smile More” and was led by Mattie Baker and Chris Luzniak. In the session, they provided various structures to promote math talk in the classroom. I am going to outline some of the ideas that I can see myself using in my classroom.

DEFENSE MECHANISMS & CLASSROOM CULTURE: Most importantly, to get talk in the math classroom involves getting over student defense mechanisms. Students fear being seen as stupid, and they fear being wrong. In order to do this, you have to lower the stakes so kids can temporarily bracket their defense mechanisms to create emotional safety. These could be by doing things like chalk talks (silently writing responses to questions, and responding to other student responses)  or doing notice/wonder activities where all responses are honored. Many of the ideas that Chris and Mattie shared in the session do this, by providing a structure for talking, and a bit of a safety net (often where no response is right, or students are required to give a particular answer and justify it).

When implementing it, you have to be consistent and do these structures fairly often. Start simple, and then get more complicated with the statements/questions. Give a lot of energy and excitement — especially if a student gives a wrong answer or a right answer (“Oh wow, what an interesting thought… let’s explore that…”). If students turn to the teacher and say “Mr. Shah, what about…” sit down and redirect it to the class. (Remember the teacher is not the center… this is about getting kids to be the center!) As teachers, we have to watch our own facial expressions (a.k.a. don’t make a face when you hear a totally wrong answer). You can avoid this (if it’s a problem for you) by looking down at a clipboard when someone is responding.

At the end of a class or a portion of a class with a lot of mathematical talk, do “shout outs” (shout out something they learned, or something someone else said that helped them). And ask kids (to fill out on a card) what they took away from class today (and what questions they still might have). Or “I used to think ____, but now I think _____.”

To give students some crutches when talking, have posters with these simple statement starters to help them (on all four walls):

TALKING POINTS: In this session I first got to experience Talking Points. I’ve read about them on Elizabeth Statmore’s blog (see links on the right… a bunch of talking points are hosted in one of her google drive folders). But the truth is: I wasn’t sure how much I could get out of them. Now that I’ve participated in one, I feel differently. This is how they work:

(1) students in a group of 4 get n statements. The first round involves one person reading the first statement, and then say “agree/disagree/unsure” and then explain why they chose that response. They must give the reason. The next person does the same, then the next, then the last. The important part about this is that no one can comment on another person’s reasons. They can just state their own reasons. They can match someone else’s reasons, but they have to be stated as their own.
(2) The second round involves the first person saying “agree/disagree/unsure” (after hearing everyone else’s thoughts) and then they can give reasons involving other people’s thoughts. Others do the same.
(3) The third round is quick and short. Each person says “agree/disagree/unsure” and gives no reasons. Then someone records the tally of the responses.

Here’s an example of what talking points can look like (when they aren’t about math content):

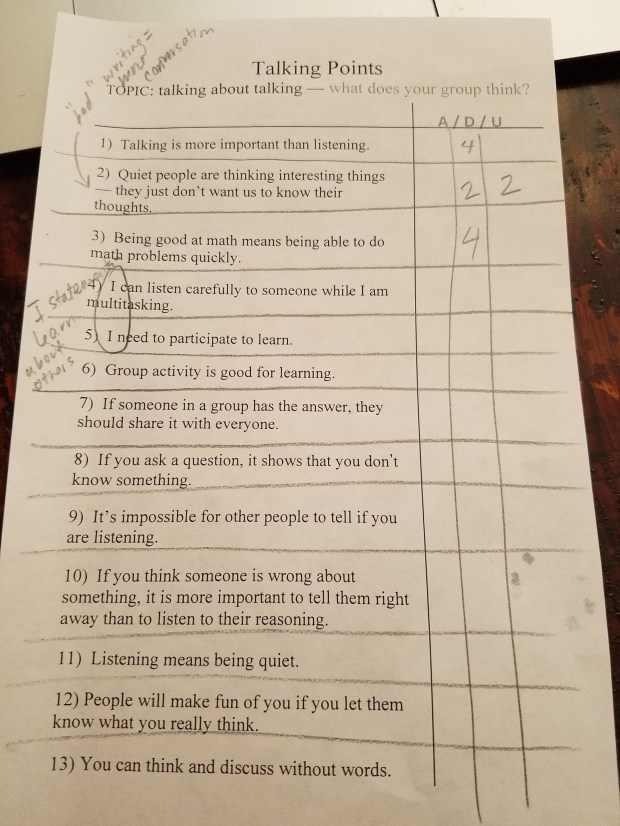
Talking points can also be math content related. Instead of “agree/disagree/unsure,” you can use “always/sometimes/never” or some variation that works for your questions. In our mini-precalculus group, we brainstormed some talking points around trigonometry:

After participating in talking points, we as a group came to the following realizations:

• Talking points were not as repetitive as we thought they would be.
• The more controversial a statement, the more discussion happens.
• You were really forced to listen to each other
• When the talking point includes “I” statements, you learn about other group members
• They are good for pre-assessments (and can be used before a unit starts, as a prelude)
• Give n statements, and then leave 3 blank statements. If a group finishes early, they can write their own talking point statements!
• Afterwards, you should have a “shout out” round. Kids should shout out something interesting/great they learned, and/or the teacher should shout out something good they heard/witnessed!

To debrief:

• Don’t go over all of the questions. That debrief will feel boring and repetative. Go over some key things you want to talk about immediately, and then revisit the others during the unit. (You want to make sure that kids don’t leave the unit with misconceptions.)
• Use the tally of A/D/U or A/S/N to see where the controversy lies! (You can collect their slips and talk about them later after seeing their responses…)

CLAIM AND WARRANT DEBATE: In a math class, you want students to justify themselves. To build that justification as central to the class, you can introduce the notions of an argument which is essentially a statement (a claim) made with sound reasoning (a warrant). (This language comes out of the speech and debate world.)

When responding to a question, a student must stand up (even the teacher should sit down) and say “My claim is _______, and my warrant is ________.” If the student messes up, that’s okay, just have them do it again. You have to build this structure as essential to answering questions. (To reduce the fear, you can give students some think time to write something down, or talk in a pair, before doing the claim/warrant step.) When doing this, I am not going to have kids volunteer… I am going to cold call using the Popsicle Sticks of Destiny (names of kids on popsicle sticks… I draw one randomly…).

When introducing claim/warrant, make sure you not only teach the structure, but also have kids who aren’t speaking face the speaker and put their eyes on them. Be explicit about the expectation. You can also have kids summarize another student’s point to make sure they’re paying attention. (If you catch a kid not following the audience instructions, you can walk over near them… if not, you can tap them on the shoulder… or kindly talk with them after class about how “it’s really polite to…”)

To build this up and create this as a routine and class structure, you should do claim and warrant debates every day or every other day at the start of the school year. Use the language “claim” and “warrant” on assessments too!

Types of questions you can ask to get kids started with this:

The best movie is ______.
The most important math topic is ______.
________ is the best method for solving the system y=2x and y=x+1.
[show a Which One Does Belong and say] ______ doesn’t belong.

Notice that each of these don’t have a “right” answer. It lowers the barrier of entry for kids.

One powerful type of question one can create are “mistake” questions. For example:

To extend claim/warrant, you can also create “circle debates” which truly forces listening. One person states a claim/warrant, and then another person summarizes that claim/warrant and then makes their own claim/warrant. This continues. It will sound like: “What I heard is that this statement is sometimes true because …. My claim is ____ and my warrant is ____.”  I think only very open ended questions would be good for this structure.

Another powerful way to extend claim/warrant is to engage is “point-counterpoint.” Let’s say the statement is: “Would you rather have crayons for teeth or spaghetti for hair?” The first person makes a claim/warrant, and the second person (no matter their true feelings) must disagree and make the opposing claim and give a warrant. Then the third person opposes the second person. Etc. It forces students to think of other points of view. In a question like “_____ is the best way to solve this system of equations” it forces students who might only approach a system in one way to consider other methods and justifications for those other methods.

CREATING DEBATE-Y QUESTIONS/STATEMENTS: Use the following words:

In the session, we took all types of questions (e.g. Graph ) and came up with debate-y questions based on it (in this example, we said “what number would you change to change the graph the most?” or “what’s the best way to graph a sine function?”). I’m not yet good at this, but I found that even with a little practice and people to bounce ideas around, I’m getting better. We had fun in my group trying to come up with debate-y questions based on this random “do now” that Chris and Mattie found online:

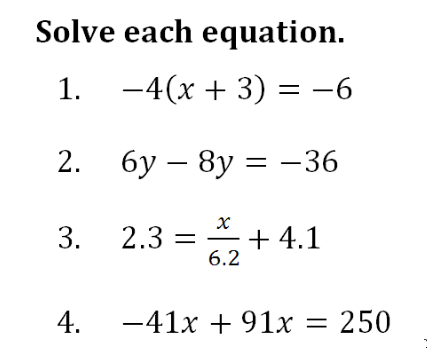
I thought it would be impossible, but the group came up with tons of different ways to convert this to a debate-y statement: (a) without solving, which is easiest to solve? (b) which would you give to your worst enemy? (c) which are similar? (d) rank from easiest to hardest? (e) a 5th problem that would fit this set of equations would be ____ (f) a 5th problem that would not fit this set of equations would be ______ (g) which one doesn’t belong? (h) give -4(x+3)=-6 and ask what the most efficient way tot solve it? and then follow up with “how could you change the problem so that method is not the most efficient?”

After a month or two, the use of claim/warrant may die down. If kids get the idea and are justifying their statements, that’s okay! It’s not about the structure as much as the idea behind the structure!

QUICKWRITE: I love this idea because I make writing integral to my classroom. You give kids a prompt and you tell kids to write nonstop for 2 minutes without editing. They have to continually write. Examples:

It can help with vocabulary, but most importantly, I see this as a way to get kids to stop overthinking and looking for “the right” answer, and just write down anything and everything without self-editing of their thinking. It’s like a condensed noticing/wondering done individually. I can be used before a debate — to give kids time to think. Or perhaps depending on the question, kids can “shout out” one part of their quickwrite? But doing it at the start of the year — to help kids get comfortable writing in math class in an non-threatening, non-evaluative manner — is such a great idea!

RUMORS:  This idea was stolen from Rona Bondi at all-ed.org. On a notecard/paper, everyone write a response to a question or a couple questions (the one we used is “what is our idea setup of our classroom?” but I think it could be used at the end of class with questions like: “One thing I find easy to understand in this unit is… One question I still have about this stuff we’ve been working on…?” or “The most important mathematical idea from today is …?” or “The best way to approach graphing trig functions is…”).

After everyone is done writing, everyone finds a parter and reads their card, the other person reads their card, and then they discuss. There is a time limit (maybe 60 seconds). Then they swap papers. Everyone finds a second partner, and they read the card in their hand to the other person, and they discuss what is written on those cards (not their own cards) and then swap. This goes on three or four times. This forces listening, it allows ideas to slowly spread, and the papers can be kept anonymous.

ONE INTENTIONAL MISTAKE: [update: a la Kelly O’Shea] Each group of students gets a giant whiteboard and a problem (it could be the same problem as other groups or a different problem). They are asked to solve the problem making one “good” mistake (so nothing like spelling names wrong, transposing a number, or labeling the axes wrong). They then present their solution to another group — playing dumb about their mistake. The other group should ask good questions to help students get at the error. Questions like “don’t you need to add 3 to both sides” is too direct… You need to ask questions which lead the group to see and understand the mistake. So perhaps “what is the mathematical step you used to get from line 2 to line 3, and why is it justified?” might be better.