This is a short continuation of the last blogpost.

In Advanced Precalculus, I start the year with kids working on a packet with a bunch of combinatorics/counting problems. There is no teaching. The kids discuss. You can hear me asking why a lot. Kids have procedures down, and they have intuition, but they can’t explain why they’re doing what they’re doing. For example, in the following questions…

…students pretty quickly write (4)(3)=12 and (4)(3)(5)=60 for the answers. But they just sort of know to multiply. And great conversations, and multiple visual representations pop up, when kids are asked “why multiply? why not add? why not do something else? convince me multiplication works.”

Now, similar to my standard Precalculus class (blogged in Nominations, Part I, inspired by Kathryn Belmonte), I had my kids critique each others’s writings. And I collected a writeup they did and gave them feedback.

But what I want to share today is a different way to use the “Nomination” structure. Last night I had kids work on the following question:

Today I had kids in a group exchange their notebooks clockwise. They read someone else’s explanations. They didn’t return the notebooks. Instead, I threw this slide up:

I was nervous. Would anyone want to give a shoutout to someone else’s work? Was this going to be a failed experiment? Instead, it was awesome. About a third of the class’s hands went in the air. These people wanted to share someone else’s work they found commendable. And so I threw four different writeups under the document projector, and had the nominator explain what they appreciated about the writeup. As we were talking through the problem, we saw similarities and differences in the solutions. And there were a-ha moments! I thought it was pretty awesome.

(Thought: I need to get candy for the classroom, and give some to the nominator and nominee!)

The best part — something Kathryn Belmonte noted when presenting this idea to math teachers — is that kids now see what makes a good writeup, and what their colleagues are doing. Their colleagues are setting the bar.

***

I also wanted to quickly share one of my favorite combinatorics problems, because of all the great discussion it promotes. Especially with someone I did this year. This is a problem kids get before learning about combinations and permutations.

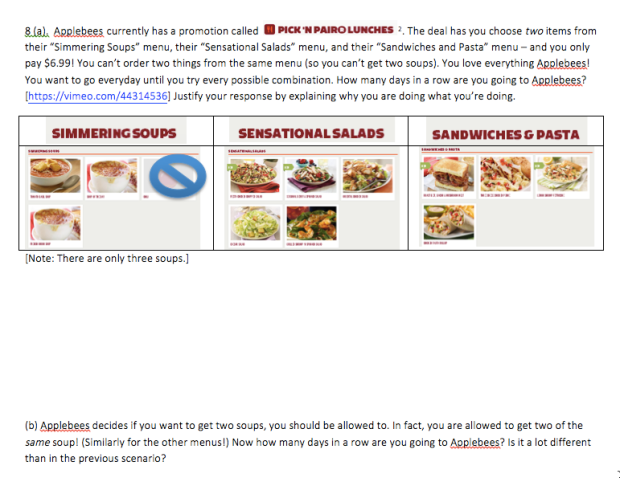
Working in groups, almost all finish part (a). The different approaches kids take, and different ways they represent/codify/record information in part (a), is great fodder for discussion. Almost inevitably, kids work on part (b). They think they get the right answer. And then I shoot them down and have them continue to think.

This year was no different.

But I did do something slightly different this year, after each group attempted part (b). I gave them three wrong solutions to part (b).

The three wrong approaches were:

And it was awesome. Kids weren’t allowed to say “you’re wrong, let me show you know to do it.” The whole goal was to really take the different wrong approaches on their own terms. And though many students immediately saw the error in part (a), many struggled to find the errors in (b) and (c) and I loved watching them grapple and come through victorious.

And with that, time to zzz.