So I’m at #TMC17 and Rachel Kernodle nerdsniped me. Or rather, I asked to be nerdsniped. Her session is at a time when there were a lot of other amazing sessions I wanted to go to, so I wanted to know if hers was one where I could hear about it and get the gist of things instead of attending. After some internal debate, she said that since it involved working on a problem, and then using that problem solving to frame the session, the answer was maaaaybe not. But then she thought: maybe I can try the problem on you and see how it goes. As long as you’re willing to put in the time to problem solve. Of course I said yes.

First, you can see her session description, which then framed how I approached the problem:

And then this is what she gave me (but it was hand drawn):

From the session description, I knew I had to find the ratio of the side lengths, so I could find exact trig values for angles other than 30, 60, 90, 45.

Rachel also gave me a “hint page” which she told me to look at when I was stuck (and to time how long it took me before I opened it). Let’s just say I’m extremely stubborn, and so as long as I think I have the capability to solve something and I am not completely stuck, I knew I wasn’t going to open it. Turns out my stubbornness paid off, and I ended up solving it.

In this post, I wanted to write a little bit about my experience with the problem. Because now when I look at that triangle, I have an duh, there’s an obvious approach to use here and everything I know points at that obvious approach. And the answer feels really obvious too. It is funny that I’m almost embarrassed to post this because there are going to be people who see it right away, and I worry (irrationally) (math pun) that they are going to judge me for not seeing it as quickly as they did. Even though I know being good at math has nothing to do with speed. And that it was important to go through the steps I did!

It took me over an hour to solve this problem. I had to do a lot of play and make a lot of random leaps before I stumbled across the “obvious approach.”  And I needed to do that in order for me to mine it for lots of things. It was true problem solving. And I know I really deeply understand this because at first the problem looked flummoxing and interesting, and now it looks obvious and somewhat trite. That’s my metric of how I know I deeply understand something. There are still certain things that I teach that I don’t deeply understand: like how the cross product of two 3D vectors yields a third vector perpendicular to the original two. I have done the math, but it’s non-obvious to me why the crazy way we compute cross products give us something perpendicular.(When I only understand something by doing brute algebra, I rarely feel like I get it.)

I’m going to try to outline the messiness that was my thought process in this triangle problem, to show/archive the messiness that is problem solving.

1. The first thing I noticed was 36 and 36 sum to 72. So I was like: obviously put two of those figures together, and just play around. Something nice will happen. I remember when seeing the problem that approach felt immediate, obvious, and would lead to the solution. I was like yes! I have an inroad! This is going to rock, and I’m going to solve it quickly! And I’ll even impress Rachel!

   

   That appraoch didn’t work. Nothing popped out. I saw 54s and 18s and 144s pop out. But those weren’t angles that helped me. But I did then realize something nice… 36 is a tenth of 360! So I was going to use a circle somehow in this solution. Obviously!

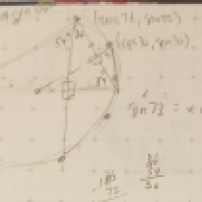
2. So I drew this:
   
   and I was like, I have something here! But after looking around, I was getting less. You can see I was trying to draw in some other lines lightly and play around — I thought maybe creating other triangles within these triangles would work. But nothing seemed to pop out. At one point, I thought I had possibly created an equilateral triangle in this (even though I saw one of the angles was 72! I was clearly desperate!). I started to get dejected at this point. I knew the circle had something to do with it…
   
3. But seeing that 54s and 18s and 36s and 72s kept appearing, I thought maybe algebraically I should play around with the numbers (adding in 180 also, since I can draw a straight line wherever) to see if algebraically I could get a 30, 60, or 45. I tried adding and subtracting numbers from the set {18, 36, 54, 72, 180} looking for 30, 60, or 45. I figured if I could somehow do that, then I could find a diagram that would have angles I could get side relationships from. And then like a domino effect, I could get others. I don’t know. But after like 2 seconds, I got bored with this and didn’t see it as very efficient. My intuition was strongly saying I was going in the wrong direction. So I stopped:

   

4. At this point, I was pretty dejected. I was slightly losing interest in the problem, thinking it was too hard for me. I tried to “force” a 60 degree angle in a diagram of that original blasted triangle. Hope! And then hope dashed!
   
   
5. Damnit! I know the circle had something to do with it. It is just too nice to abandon the circle! Maybe…
   

   

   

   At first I drew all ten vertices for a 10-gon. I started connecting them in different ways. I thought I could exploit the chord-chord theorem in geometry, but that wasn’t good. I tried in that second diagram to extract part of the circle diagram and investigate it more. And the third was just more of the same. At one point, I was like and was thinking I could somehow think of this as a problem on the complex plane, where each vertex was and then look at the real parts for the x-coordinate and the imaginary parts for the y-coordinate. Clearly my mind was whirring, and I was going anywhere and everywhere. I actually thought maybe this complex plane thing seems ugly but it will be so elegant. But then I realized I didn’t know where to go if I labeled each of the points on the complex plane. Done and done and done. At this point I put the problem away. Nothing was working.

6. But after a minute, I couldn’t let it go! I wanted to solve it!!! So I went back. I thought I was getting too complicated, so I went simple.

   

   Nope. Didn’t help. But for some reason, this diagram and looking at the 72 reminded me of something I hadn’t thought of before. This is the leap that helped me get to the answer. And I can’t quite explain why this diagram sparked this leap. Which sucks because this is that moment that led to the rest of the problem for me! But I immediately remembered something about 72s and pentagons. And it hit me.

7. So I drew what this connection was. My brain was whirring, and I was somewhere good…  
   

   I remembered the 72 degree angle appeared in a star. And this star was related to a pentagon. And that the pentagon had something about the golden ratio tied up in it. So I knew that maybe the golden ratio was involved in the answer. And where does the golden ratio appear? When there are similar triangles and proportions. I had my new approach and my inroad that I thought would work. Two triangles next to each other failed. Circles failed. But star/pentagon might work!

8. So I looked at the original triangle and tried to figure out where I could find a similar triangle. And so I drew one line and created a similar triangle. I labeled the two legs as having length “1.”
   

   Initially, I was thinking I could do something with the law of sines. Because if you think about it, this is the ASS case — where you have that 36 degrees (circled), the side I labeled 1 (circled), and the other side I labeled y (circled). But you note that last side could be in two different places, which is why there are two ys circled. I still think there is something fun that I could do with this. But as I was doing this, I realized I was making things more complicated.

   I knew that the golden ratio came out of a proportion. So I abandoned the law of sines for the proportion. I simply set up a proportion with the two similar triangles. I first found “?” by doing . So ? was . This was exciting. I knew the golden ratio came out of solving a quadratic. Yeeeeee! At this point, my excitement was growing because I was fairly confident I was almost at the solution.

   Then I labeled the part of the leg that wasn’t ? as (since the whole leg length was 1). Finally I looked at the third triangle in the diagram that wasn’t similar to the original triangle. It was isosceles and has legs of and so I set them equal and solved and not-quite-the-golden-ratio came out! (There was a mistake I made where I set and got . But I then found it and rewrote the equation . This was the most depressing part of it. Because I couldn’t find my error because I was so tired. I went through my work multiple times and nothing. But taking some time away and then looking with fresh eyes, it was like: doh!)

   And so that was the end. I found if the original triangle had leg lengths of 1, the base was going to have a length of .

   I was so proud. I was on cloud nine. I was telling everyone! SO COOL!!! 

It probably took me in total 90 minutes or so from start to finish. So many false starts at the beginning, and one depressing transcription error that I couldn’t find.

The point of this post isn’t to teach someone the solution to the problem. I could have written something much easier. (See we can draw this auxiliary line to create similar triangles. We use proportions since we have similar triangles. Then exploit the new isosceles triangle by setting the leg lengths equal to each other.) But that’s whitewashing all that went into the problem. It’s like a math paper or a science paper. It is a distillation of so freaking much. It was to capture what it’s like to not know something, and how my brain worked in trying to get to figure something out. To show what’s behind a solution.