Good Math Problems

Pendulum Lab, Reprise

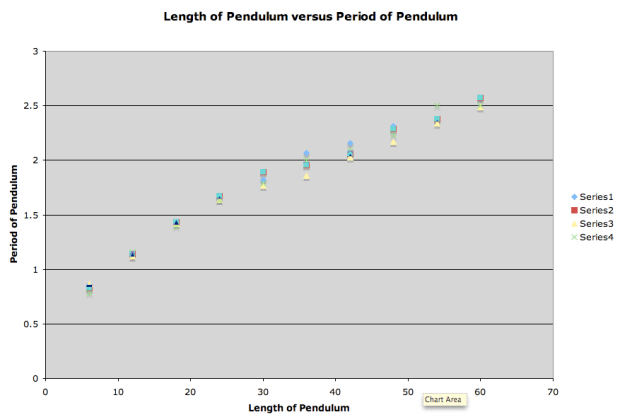
This post refers to the pendulum lab I recently posted about. I had my students collect data, and this is what they got:

Length (inches)

Period (sec): Group I

Period (sec):
Group II

Period (sec):
Group III

Period (sec):
Group IV

60	2.57	2.57	2.49	2.50
54	2.36	2.38	2.34	2.50
48	2.31	2.29	2.17	2.23
42	2.16	2.06	2.03	2.09
36	2.07	1.96	1.86	2.00
30	1.82	1.89	1.77	1.79
24	1.64	1.67	1.64	1.63
18	1.44	1.43	1.42	1.39
12	1.12	1.14	1.12	1.16
6	0.86	0.83	0.87	0.78

The data was pretty consistent among the various groups. Remember we did this lab in the context of parabolas. However, when the groups plotted their results, they were getting:

What?! The data doesn’t look quadratic. If anything, it looked to us like a square root or a quadratic with a negative $x^2$ coefficient. We used our calculators to do a quadratic regression, and got (for one set of data):

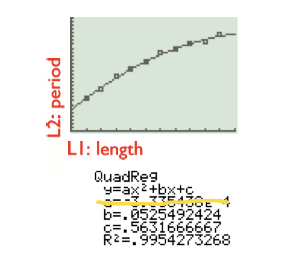I tricked my class into believing this was a good model. I mean, look at it! The parabola fits the data so well!

But then we looked at the $x^2$ coefficient and saw it was negative and nearly zero. And then when we expanded our domain, we got:

It was at that point that students saw how our model sucked. Because they said that if we increase the length of the pendulum, the period should increase too.

So we went back to the drawing board. I suggested that we plot period versus length, instead of length versus period. (Next year I’m going to have us discuss this idea more — the swapping of x and y coordinates, and how something that looks like a square root might look like a parabola if we do that. Because of timing issues in this class, I just told them that was what we were going to try. Sigh.)

And we did, and found the quadratic that modeled it, and saw:

And then we extended it to see that if we increased our period, if the length would increase too…

It does! It makes conceptual sense too! (We also talked about whether it should hit the origin and why our model does or does not hit the origin.)

With our newfound analysis, I had students answer the following question based on their “good” quadratic model (in our case above: $y=10.57x^2-4.62x+2.85$ ):

(a) If your pendulum has a period of 1.5 seconds, estimate the length of the pendulum.
(b) If your pendulum has a period of 20 seconds, estimate the length of the pendulum.
(c) If your pendulum has a length of 10 inches, estimate the period.
(d) If your pendulum has a length of 1,200 inches, estimate the period.

What is nice is that (a) and (b) just involve students plugging in $x=1.5$ and $x=20$ into their model. And all the groups got very similar answers for the first length, and really different answers for the second length. So we got to have a short (I wish it could have been longer) discussion of why that is so. (We talked about interpolation versus extrapolation.)

And then (c) and (d) involved students solving a messy, real world quadratic because they’re setting $y=10$ and $y=1200$ . The same thing that happened in part (a) and part (b) happened in part (c) and part (d); all the groups got very similar answers for the first period, and really different answers for the second period.

What we didn’t get to talk about, unfortunately, is the theoretical answers, based on physics. The formula for the period of a pendulum is $T=2\pi\sqrt{\frac{L}{g}}$ where $T$ , $L$ , and $g$ are in standard metric units. So I was hoping we’d get a chance to do some unit conversions to see how our experimental data relates to to theoretical data.

I did get to show my students how their values compared with the theoretical data:

Length of String	Group 1	Group 2	Group 3	Group 4	Theoretical
60	2.57	2.57	2.49	2.50	2.48
54	2.36	2.38	2.34	2.5o	2.35
48	2.31	2.29	2.17	2.23	2.21
42	2.16	2.06	2.03	2.09	2.07
36	2.07	1.96	1.86	2.00	1.92
30	1.82	1.89	1.77	1.79	1.75
24	1.64	1.67	1.64	1.63	1.57
18	1.44	1.43	1.42	1.39	1.36
12	1.12	1.14	1.12	1.16	1.11
6	0.86	0.83	0.87	0.78	0.78

I think they were impressed, though I didn’t get the ooohs and aaahs I was hoping for. I’ve plotted the theoretical (purple) with the actual data (yellow) so you can see how good the experiment was. I am not plotting it on a period versus length graph, though if I were to show my students, I would do that because that’s the way we analyzed the data (we got a parabola).

And with that, we finished our lab.

Moore’s Law

The Technology Review magazine has an arresting photo essay on Moore’s Law — as told through a bunch of stunning pictures of computer chips. Click on the link above to see all the other circuits. For those who don’t know, Moore’s Law says that about every two years (some say 18 months), the number of transistors that can fit on a circuit doubles (for Wikipedia article, click here).

The only thing I wish about the photo essay is that there was some sense of scale for each picture. Regardless, the captions tell the year each circuit was created, and the number of transistors on each circuit. The data are:

1958	1
1959	1
1961	4
1974	5000
1979	68000
1978	29000
1985	275000
1991	200000
1993	3100000
1993	2800000
2000	42000000
2007	410000000
2009	758000000

So of course, even though this data isn’t perfect nor complete, I thought I’d see how it’d look graphed.

Ohhh, it looks like it could be exponential… Let’s plot it on a log-scale. If it’s exponential, we should get a straight line:

Ohhh, this looks pretty linear! I wasn’t sure that it was going to work out.

The exponential line of best fit is: $Transistors=e^{0.397*\text{Year}-777.29}$ . When I plot the data (pink) and the exponential line of best fit (blue) on the log-scale graph, you’ll see that Moore’s Law looks like it has some serious bite to it.

Doing a little algebra with the exponential model we came up with, it appears that the number of transitors doubles about every 1.75 years.

And if you cared, Wikipedia gives their own following graphical illustration of Moore’s Law:

I’m going to be teaching exponential functions in a bit. I hope we’ll have time to do regressions. If so, I’ll probably make a 2-day investigation out of Moore’s Law.

Other posts I’ve made about logarithmic and exponential functions:

Logarithmic Graph in the News
Earthquakes, Richter Scale, and Logarithms
The Supreme Court, Linear and Exponential Growth, and Racial Segregation
The Origin of Life on Earth and Logarithms
Paper Folding and Exponential Functions

Digital Artifacts

Dan Meyer has recently been asking teachers to consider (a) the problems with textbook application problems and (b) finding or creating compelling content for the classroom.

I’ve been thinking about this since he’s started posting, and I’m trying to think of where I can find — but not create — the interesting digital media that would satisfy his criteria.

In the meanwhile, I decided to look on youtube for some videos that would naturally lead to a particular discussion/topic for some high school math class. Some are better than others. Without further ado…

Inequalities and Quadratics

In Algebra II,, we’ve recently been delving into quadratics. I recently blogged about how I taught completing the square and the quadratic formula, and put up a bunch of resources. Since then, we’ve moved on to graphing quadratics, followed by inequalities.

The complete topic list for inequalities is:

I’ve been trying something new, which is creating packets for students to work on. In essence, I’m creating my own textbook for these sorts of questions. I thought I’d share them with you in case they prove useful [1]. I’m pretty proud of them — and they way they fit together and build up understanding, not just providing a method to solving problems.

1. PACKET 1: Linear and Quadratic Inequalities on the Number Line (PDF version)
2. Additional Homework on Quadratic Inequalities (PDF version)
3. PACKET II: Linear and Quadratic Inequalities on the Coordinate Plane (PDF version)

4. PACKET III: Systems of Inequalities (Linear and Linear-Quadratic) (PDF version)
5. Additional Homework on Systems of Inequalities (PDF version)
6. Pop Quiz on Inequalities and Quadratics (PDF version)

Hopefully they’ll be useful to someone else out there!

[1] The formatting might be a bit off for you… It looks slightly off (meaning the pages don’t end where I intended them to end) on my mac but fine on my PC. I think you need to make sure that on a Mac you select all and convert the font to “Gill Sans” (on a PC, I think it’s called “Gill Sans MT”, which is creating the problem).

UPDATE: PDFs posted, without typographic weirdnesses.

dy/dan’s Annual Report Results

First Place: Ben Wildeboer

Second Place: Frieder Knauss*

Third Place: Simon Job

Dan Meyer’s Favorites: Frieder Knuass & Sam Shah (that’s me!)

To determined First, Second, and Third place, Dan had each entrant send in their favorite top 3 annual reports, in order. So Dan was using some form of preferential voting — which could have led to disaster. How, you ask? Well, it’s a bit of an interesting paradox.

Say we have 3 people ranking 3 candidates (A, B, and C).

PERSON 1: A B C (in that order)
PERSON 2: B C A (in that order)
PERSON 3: C A B (in that order)

Who wins? The great Englightenment thinker Condorcet noted this paradox.
*Mr. K’s (Frieder Knauss) annual report was my #1 favorite. If you want to read why, click on the “Second Place” link above. My blurb is posted there. Part of my interpretation wasn’t correct, as Mr. K points out on his blog.

What can you do with this?

Dan Meyer of dy/dan fame has a series of posts titled “What can you do with this?” — where he shows a picture or video with some sort of math connection, and asks teachers how they might use it in class. (Others are jumping on the bandwagon.) I figured why not. I love the idea. What I’ve noticed is that many of the pictures deal with ratios and proportions. I wonder if we can get pictures that deal with other things — like radical equations and limits.

Michael Lugo at God Plays Dice directed me to the following picture:

Fantastic, isn’t it! What you could do in a math class isn’t obvious at first glance. But let’s see what you come up with! For a spoiler (do NOT check it out until you’ve come up with an idea yourself), see below the jump.

(more…)

Venn Diagrams and Formulas

At the math office today, two math teachers were discussing probability. Two things were surprising about it. One, it was a Saturday afternoon part of our winter break, so no teachers should have been on campus. (We’re a dedicated lot, us math teachers.) Two, the topic they were discussing was so simple, and yet, it reveals the real mind-bending character that probability has on us and our students.

Question 1: What is the probability that you draw a heart or a queen from a deck of cards?
Question 2: What is the probability that you roll a die and get a number less than 4 or an odd number?

Both questions are simple enough. The first one is 16/52 (because there are 16 cards which are hearts or queens in a deck). The second one is 4/6 (because you can roll a 1, 2, 3, or 5).

The problems are seemingly the same. Let’s now look at this problem from the perspective of a venn diagram.

If we want to know the probability that event A or event B occurs, we clearly can see that we have:

$P(A\text{ or }B)=P(A)+P(B)-P(A \text{ and } B)$

(We have to subtract that last term, because we added that overlapping section twice when we took $P(A)+P(B)$ .)

Let’s apply that to our two questions:

Question 1: We have a probability of: $P(\text{Heart or Queen})=P(\text{Heart})+P(\text{Queen})-P(\text{Heart and Queen})$ . Clearly $P(\text{Heart})=13/52$ and $P(\text{Queen})=4/52$ . What is $P(\text{Heart and Queen})$ ? Intuitively — or using our venn diagram — we know it is 1/52. And the answer works out correctly to 16/52.

Question 2: We have a probability of: $P(\text{less than 4 or odd number})=P(\text{less than 4})+P(\text{odd number})-P(\text{less than 4 and odd number})$ . Clearly $P(\text{less than 4})=3/6$ and $P(\text{odd number})=3/6$ . What is $P(\text{less than 4 and odd number})$ ? Intuitively — or using our venn diagrams — we know it is 2/6. And the answer works out correctly to 4/6.

However, let’s say we wanted to calculate $P(\text{Heart and Queen})$ and $P(\text{less than 4 and odd number})$ (the overlapping regions) mathematically? It turns out that there is something fundamental that makes these two problems different. In question 1, the two events (drawing a heart / drawing a queen) are independent. In question 2, the two events (rolling a number less than 4 / rolling an odd number) are dependent. For the first question, you can say that $P(\text{Heart and Queen})=P(\text{Heart})P(\text{Queen})$ while in the second problem you cannot do that.

Recall that the definition of independence of two events $A$ and $B$ is if $P(A|B)=P(A)$ .

Checking the first question for independence, we see that the probability of drawing a heart given that you already have a queen is 1/4, and that is the same as the probability of drawing a heart (1/4). (Similarly, the probability of drawing a queen given that you already have a heart is 1/13, and that is the same as the probability of drawing a queen (1/13).) So the two events are independent.

Checking the second question for independence, we see that the probability of rolling and odd number given that you have rolled a number less than 4 is 2/3, while the probability of rolling an odd number is 1/2. (Similarly, the probability of rolling a number less than 4 given that you’ve rolled an odd number is 2/3, while the probability of rolling a number less than 4 is 1/2.) So the two events are dependent.

The teacher who brought up this problem was grading exams, and one student had calculated $P(\text{Heart and Queen})=P(\text{Heart})P(\text{Queen})$ . And seeing the two problems were almost identical, calculated $P(\text{less than 4 and odd number})=P(\text{less than 4})P(\text{odd number})$ — which, as we know, isn’t right for dependent events.

What we were discussing is how we could explain to the student that the two situations are different, even though on the surface the questions seem like they are of the same form. In other words, is there a conceptual — non mathematical — way to explain that the first question involves independent events while the second question involves dependent events? It certainly isn’t intuitive, at least not to me.

Continuous Everywhere but Differentiable Nowhere

I have no idea why I picked this blog name, but there's no turning back now