Good Math Problems

A great Multivariable Calculus problem

Today I gave my multivariable calculus class a problem — a problem I give every year, that I found… somewhere. Maybe MIT, maybe an Exeter problem set, maybe a textbook. And if you ever want to see kids work together, and do some good problem solving, this is a prime problem for that.

Up to now, we’ve been working on vectors — and they learned vector basics (read: dot product and cross product). Here’s the question.

You have any tetrahedron. Sticking outwards from each face, orthogonal to each face, is a vector with magnitude equal to the area of face it is sticking out of. Prove that if you add these four vectors together, they sum to the zero vector.

It’s such a beautiful problem. I don’t have a totally geometric way to explain why this is true (we do lots of good vector algebra), but I do enjoy watching everything all come together. To me, it almost works like magic.

I then had a student ask an amazing extension question. (If they’re asking extension questions, you know it’s a rich problem.) He said: “Will this always work for any polyhedra? What about figures involving faces which aren’t triangles?” I, of course, decided I loved the problem. And I desperately want him to work on this for his final project.

I love the idea of this student taking this problem and seeing how far he can run with it. I mean: hello, gluing tetrahedrons together! (I expect him to make some stick models, if he does it!)

Exasperating Problem

So a while ago, I mentioned to some of you on twitter that I was getting really frustrated with a particular problem we were presented with. I have a conjecture that I’m almost certain is true, but I can’t prove it.

Consider the unit circle x^2+y^2=1. Plot n equally spaced points on the circle starting from (1,0). Now draw the n-1 chords from (1,0) to the others. What is the product of the lengths of all of these chords?

(There is an extension problem, which is changing the unit circle to an ellipse 5x^2+y^2=5, for those who already have seen or find the original problem too easy.)

So feel free to write your own blog post with your solution, or throw your solution in the comments (just write SPOILER at the top so we know…).

What I’m interested in is if we could get a precalculus class to get the solution to this problem. Where they actually understand it. So if you had, say, 15 non-honors precalculus students and one week to work on this problem, how would you design the lesson?

I guess you have to have solved it or have seen a solution to know how to design the lesson. But even if you didn’t solve it (a la me!)… if there’s a solution you’ve read that someone posted in the comments… what would you do?

UPDATE: Mr. Ho has a great GeoGebra applet at his site; Mimi has some nice colorful diagrams and some explanation up at her site. Also, for those who want to wording for the ellipse problem… This extension I haven’t seen before, so I am citing Bowen Kerins (see comments below!) or Darryl Yong: “Take the diagram you drew in [the unit circle problem] and stretch it vertically so that the circle becomes the ellipse 5x^2+y^2=5. All the points for the chords scale too. What is the product of the lengths of all of these chords?”

Using a Cannon to Kill a Fly

Dan Meyer, in one of his recent WCYDWT, posted a picture of a roll of tickets (among other annuli).

So obvious is the question: how many tickets?

Of course more questions come tumbling out immediately, questions we need to ask to figure it out. What’s the inner and outer radius? What’s the length of one ticket? What’s the “thickness” of a ticket?

Dan sent me the information:

Inner Diameter: 27.77 mm
Outer Diameter: 168.65 mm
Length of a Ticket: 51.21 mm
Thickness of a Ticket*: 0.22 mm

The easy way to solve this is to find the area of the Annulus (the green area) and divide it by the area of the side of one ticket.

Of course the area of the red ticket is the “thickness” of the ticket multiplied by the length of the ticket.

I put the ticket on the side, lying flat on a table. So the height of that rectangle is the thickness of the ticket (exaggerated for dramatic effect) and the width of that rectangle is the length of the ticket. And you can see how that rectangle becomes curved when it is part of the roll.

Clearly if we want to find how many tickets can be curved to form the entire green roll, we’ll simply have to find the area of the green roll (the annulus) and divide it by the area of a single ticket.

Using Dan Meyer’s numbers, we get the number of tickets to be:

N=\frac{\pi(168.65/2)^2-\pi(27.77/2)^2}{51.21*0.22}

This comes out to be about 1929.07 tickets.

(The true answer is 2000 tickets).

But sometimes you want to kill a fly with something more powerful than a fly swatter. Something that will be slightly more challenging. Chopsticks? Been done. A cannon? Hard to find them lying around. Calculus? OF COURSE!

(Also, Dan asked if there was a way to solve this with Calculus.)

I had a couple ideas, but the most interesting for me was to try to come up with a function to model the tickets being rolled around a tube.** If I could find an equation which twists around like a roll of tickets, I could then use calculus’ arc length formula. If you don’t know what that is, it is pretty darn powerful. Given any normal function — curvy, straight, you name it — you can find how long the function is!

The idea behind it is the idea behind most calculus ideas. Break up the function into a bunch of pieces, and approximate the pieces with lines segments. Then add the lengths of those line segments together. You have an approximation for the true length of the function. If you break the function into more and more pieces, your approximation gets better. And if you start breaking the function into an almost infinite number of pieces and adding those line segments together, you’re going to get an almost perfect length. That’s calculus, and I’m not going to go into how you add an infinite number of line segments together here, but don’t be daunted. It sounds much more difficult than it is in reality.

Regardless, the whole point here is if we can find a function to model the tickets being wound around and around and around, we can just apply the calculus arc length formula and find the length of all the tickets if they were rolled out!

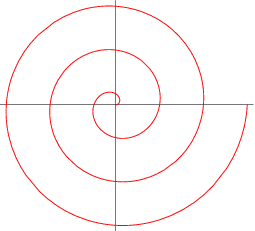
So the hard part about this problem is coming up with the equation to model the rolled up tickets. But it’s just a spiral. In particular, an Archimedean spiral.

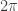In polar coordinates, the equation to get this spiral is the SUPER simple: r(\theta)=k\theta. You can’t get much simpler than that. It obviously takes 2\pi radians to make one full circle (to start and end at the same angle). And in that 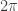2\pi radians, the spiral moves out from it’s previous location 2\pi k. That’s all we need. Seriously.

So first we’re going to model the ticket roll as if it does not have that hole in the center. It’ll first just be a spiral that will go on and on forever. We’ll then find where to start and stop this spiral to create the roll of tickets which starts at some inner radius and ends at some outer radius.

Look at that Archimedean spiral one more time. For our purposes, I want the distance between the red lines above to be the thickness of a single ticket. Does that make sense? That way the ticket’s are getting wound around and around and around, laying on top of one another.***

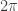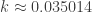Remember that for each total revolution (2\pi), the spiral moves outwards 2\pi k  from it’s previous location. We want that distance it moves outwards to be the thickness of the ticket. So we simply set the thickness (0.22 mm) equal to 2\pi k to find that k \approx 0.035014.

HOLLA! We now have the function we’re using to model the tickets:

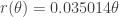r(\theta)=0.035014\theta.

Dude, graph that on your TI-whatever and you’ll see a nice tight spiral.

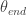Now to start and stop the spiral so it matches our roll of tickets. To do this, we need to graph it for only certain \theta values — so that we can get the spiral to start at the inner radius and stop at the outer radius. That’s just simple algebra, boys and girls! We’ll call the starting angle value \theta_{start} and the ending angle value \theta_{end}.

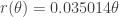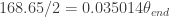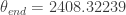Since r(\theta)=0.035014\theta, we want to know what \theta is that will bring the spiral out to the inner circle. That will be our starting angle! So 27.77/2=0.035014\theta_{start}. Similarly we can set 168.65/2=0.035014\theta_{end}. The starting and ending angles are easily solved for, to get \theta_{start}=396.55566 and \theta_{end}=2408.32239.

Graphing the spiral with these endpoints looks like:

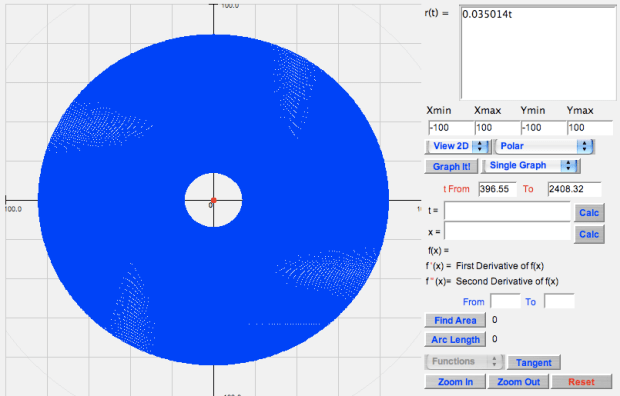
We’ve done all the hard parts! Now we simply use the arc length formula in calculus (for polar equations) to find the length of the spiral! Again, I’m not going to explain the derivation, but the equation for arc length is:

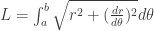
L=\int_{a}^{b} \sqrt{r^2+(\frac{dr}{d\theta})^2} d\theta

This gives us the length of a function, from one endpoint to another. Applying our equation for r(\theta) into this, we get:

L=\int_{396.55566}^{2408.32239} \sqrt{(0.035014\theta)^2+0.035014^2} d\theta.

Using the calculator to solve this, we get 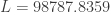L=98787.8359  mm. That’s the whole length of the roll of tickets, if it the tickets were laid out flat instead of rolled up. So by simply dividing this by the length of a ticket (51.21 mm), we get the number of tickets.

This comes out to be 1929.07 tickets. That’s what we got with calculus.

It seemed a bit crazy to me that the answer without calculus would be identical to the answer with calculus. It took a few minutes of thinking, but then it dawned on me that it would be crazy if they were not identical.

I wrote to Dan Meyer, explaining that I got the same answer using calculus that he did without, and that ex post facto, of course it made sense. I said:

Once I saw that we got the same answer, it dawned on me that they SHOULD be the same answer. (Isn’t that always the way in math?) Why wouldn’t they be the same? We’re both using the same initial data (inner radius, outer radius, thickness, and ticket length), and we’re not approximating anywhere in our calculations (we’re being exact).****

So there you go.

I just love that this simple algebra solution and this calculus solution turn out to be the same. Instead of showing me how useless calculus is (why do we need it if we can do it without?), I can’t help but cogitate on how amazing calculus is! These two methods are completely different! One is geometry. The other is based in functions. But both solutions are reducible to the same thing. They are really the same thing.

Now if you’re a calculete and you’re really interested in finding an exact — and non-calculator based solution — to the arc length integral, I suggest you look at the bottom of this page. It’s not hard, but also not the point of this post. I wanted to make the general process clear to someone who might not know calculus, but interested in the idea of how we can use it to solve the same problem. Of course, it’s a bit silly, way more firepower than you need. But it really gets you thinking about the ideas undergirding calculus, and there’s where I see the value in doing explorations like these.

PS. If you’re wondering why we’re not getting 2000 tickets, I think the answer is simple. In the initial data (the inner radius, the outer radius, the length of a ticket, and the thickness of a ticket), there was probably some error. I suspect it was with the thickness of the ticket — the hardest thing to actually measure. If the thickness of aticket was found to be 0.2124 mm (instead of 0.22 mm), then we would get precisely 2000 tickets! So if Dan were able to measure to the hundredths or thousandths accurately, I bet we would get something way closer to 2000 tickets.

—

*I seem to recall that Kate Nowak Jason Dyer suggested removing a bunch of tickets (50?) from the roll, stack them up, and measure the height. Use that to get the approximate thickness.

**Of course concentric circles would be possible, but then you’d get a summation, and blah blah blah. It all seems more precalculus than calculus.

***If that doesn’t make sense, try looking at this horrible picture of a shrimp. I mean ticket roll.

**** If you say I rounded to 5 or 6 decimal places a few times, guilty. However, I actually calculated it without any rounding, and it comes out to be the same value. So there. Pfft. The rounding didn’t affect the answer to the hundredths place.

Histograms, Standard Deviations, and Digital Cameras

Our last unit in Algebra II was statistics — and it was a hurried unit. (As last units always are.)

One of the topics I was covering was histogram basics. And I wanted to make it somewhat interesting. So I went online, and came across a page which explained how to understand histograms that your digital camera produces. You know what I’m talking about, right?

That’s the one. How do you get it on your camera? Heck if I know. I just pushed a lot of buttons and eventually the histogram appeared.

Because I had about 20 minutes, I just lectured my kids on how this histogram worked.The histogram has 256 columns (numbers 0 to 255). Each pixel on your camera is assigned a number from 0 (representing pure darkness) to 255 (representing pure lightness). Then the height of each bar represents the number of pixels with that particular level of darkness/lightness.

By that one little piece of information, you can start telling a lot about a photo. Such as when it is over-exposed and under-exposed, and when there is too much or too little contrast. You might wonder how photo editing software can increase the contrast or correct for a photo being over/under-exposed. One you learn about this, the answer is pretty simple. The program reassigns each pixel with a different brightness.

See examples that I cribbed from the website on my smartboard. Pay special attention to how the over-under exposed histograms differ from the “ideal” histogram (and similarly for the too high/too little contrast):

I really enjoyed learning about this, and sharing what I learned with my students. But next year, I want to do something more. I want students to take photos and play with them in some image editing software — and see what happens to the data as they modify the image in certain ways. What does brightness mean? Will things change if the image goes from color to black and white? What does sharpening the image do to the histogram? I want them to talk about mean, median, and mode — and how they change. I want them to talk about standard deviation — and how it changes. I want them to talk about range and shape — and how they change. I want them to make a short writeup explaining their findings.

Look at what Picasa (free) offers:

You get the histogram (bottom left)! You also get all these ways to modify the picture!

And the histogram changes as you modify it! In REAL TIME as you slide sliders!

I don’t know quite yet how to make this rigorous or ways to ensure they’re learning. It’s kinda bad, because I just want to play around with this and discover what all these things do myself, not knowing what I want them to get out of it. I just want to explore. I’m not thinking backwards. But I suspect a good short bit on the shape of data can be made from this. (Alternative reading: I wouldn’t begrudge any of you if you, say, went out and made a short unit based on this and sent it to me.)

Binomial Theorem Video Contest

Kate Nowak’s binomial theorem video contest deadline is this Thursday! Which means you still have time to enter. It’s not about perfection, or about video length, but about coming up with an interesting idea and trying to execute it. Don’t feel bad about the competition bit — and thinking your idea isn’t good enough, or that it’s been done before, or that you can’t make a professional-looking video, or that you think it’s too boring. Just put caution to the wind and throw your hat in the ring! I think everyone in this online-math-teacher-edu-blogosphere-thingy is probably a bit too critical about themselves, and always feels a little inadequate. (I know I do. All. The. Freakin’. Time.) This is about just experimenting and trying something out.

And yes. You obviously can win fame and glory. And an ill fitting t-shirt. And possibly (if there are 7+ entries) the Lemov book. There’s that too.

Factoring Quadratics by Grouping

David Cox teaches “Bottom’s Up” to show how to factor quadratics. (Video here.)

There’s only one thing I don’t like about this method. It has one step which isn’t intuitive, and makes it all seem like magic.

When you have a coefficient in front of the x^2 term that isn’t one, you have to divide the factors by that number. And then you do “bottoms up” where the (x+\frac{1}{2}) gets converted to (2x+1). I don’t like that you have to randomly divide by a number, nor that the implicit implication is that (x+\frac{1}{2})=(2x+1).

A fellow math teacher at my school taught me to teach a very similar method, but that uses factor by grouping.

Given a quadratic, the first part is the same:

2x^2+7x+3

Rewrite the 7x as 6x+1x (numbers from the diamond above)

2x^2+6x+1x+3 [1]

Then the problem becomes a “factor by grouping” problem. You group the first two terms and second two terms and factor:

2x(x+3)+1(x+3)

Then you see each term has an (x+3) so you factor that out and are left with (2x+1):

(x+3)(2x+1)

It might seem a little more complicated, because you have to factor a few times. But my kids tend to get it after practicing 3 or 4 problems, and it doesn’t involve any knowledge they didn’t already possess. They understand that 7x=6x+1x and they understand how to factor 2x^2+6x. There is no lingering “why?”

[1] You could write it 2x^2+1x+6x+3 also and it would work. 2x^2+1x+6x+3=x(2x+1)+3(2x+1)=(2x+1)(x+3).

A binomial expansion throwdown. You in?

Oh k8, my k8, has thrown down the gauntlet. Or in more modern day kid-speak, she asked you to “BRING IT ON!” (That’s Kate Nowak, for y’all.)

A while ago, she scoured every nook and corner online for videos teaching the binomial expansion, or for some ideas which make the teaching of it… well… not excruciatingly boring. Actual videos that didn’t make her want to stab her eyes out, they didn’t quite exist.

So she’s asking you to: make one. Anything that’s better than what’s out there.

You have weeks to do it (deadline: May 27th). She’s offering some sort of t-shirt prize. I’ll sweeten the pot. If we get 7 or more video submissions, I’ll buy the winner a copy of that Lemov book that the New York Times article featured a few months ago (as long as you don’t live somewhere with crazy shipping costs). And if you own that (or don’t want it), I’ll buy you some insanely cool math book. Yes, this is my own money. No, I don’t know why I’m doing this, since I’m pretty poor.

So when Kate says “BRING IT ON!” I hope you enter so you can say “IT’S ALREADY BEEN BROUGHTEN!”

Also, if you have a math or math teacher blog and want to spread this around, that would be super duper awesome.