Monthly Archives: July 2008
The Video Verdict: Check Plus!
PREAMBLE
One of my friends is in Paris, helping set up an art installation by Ryoji Ikeda on the number “e”. And I received a frantic email from her asking for help understanding set theory, e, and infinity.
I sent her information on set theory and e via an email and links, but not on infinity. There are a number of good books and articles on it, making it accessible to a layperson. But I found this youtube video which is directed to the hoi polloi.
There are bits of the presentation that could be improved (the jokes are not really played well, I see quick and easy ways to make it more “mathy”). But these small things don’t take away from the fact that it is a darn good presentation. And darn it, now I want to give a presentation on infinity! Oh well.
THE CRUX
Interestingly, making the decision to email my friend the video instead of articles gets at the heart of the problem that dy/dan and others are grappling with: when is video an appropriate teaching tool – and is it better?
There are two poles outlined by dy/dan:
- Video is personable and injects human qualities that can’t be gotten from a text. These human qualities help enhance the learning process, by improving understanding.
- It takes a heck of a lot more time to watch a video on math than it does to read a paper which goes through the same math (efficiency argument). Reading also allows students to learn at their own pace, go back to sections they didn’t get, and active.
I thought these poles were meant to be generally taken for video in classroom instruction, even though the examples used were videos from leaving comments in blogs…
So let’s get this out of the way: context is everything, and there isn’t a single answer. Nor is anyone really looking for “an answer.”
With this said I strongly believe the second point is a red herring, and the first is really crucial. I evidence it with a counter-example-question:
Why do I even need to be in the classroom? If students-at-large can learn the content we want them to learn by reading the textbook, do I even need to be there? What am I doing at the board? What am I doing walking around the classroom? I hope (pray!) that it’s not only to answer questions that the book doesn’t address or when they get stuck… because otherwise, why bother showing up?
Teaching with talking, with dynamic visuals (instead of static pictures), with caveats and asides that aren’t easily worked into a text, with auditory and kinesthetic elements… many, many students respond to that. They engage with that.
(Not that I’m saying students can’t read actively or can’t learn from books… but there is something that books can’t capture that we teachers can.)
I guess what I’m saying is this: I see a defense of the need for good teachers in the classroom to also be a defense of video. (If well chosen/done.)
And I honestly think that almost everyone would agree with that.
NOTE AND CONFESSION: A PLEA
I suspect (but can’t be sure) that most of the discussion about video in the edblogosphere is not talking about videos of a lecture or solution to a problem… but I think that my thoughts about this may still hold. I’m honestly wondering though if those blogging about videos in the classroom have a firm sense of what videos they are talking about? I’m sure they aren’t trying to kick a dead horse by arguing against this type of valueless video:
But if they aren’t talking about these terrible videos, or videos about teaching, or lecture videos, or videos of how to solve a math problem, or small video clips to motivate a class discussion, I’m a bit clueless about what videos they’re talking about. I just don’t know. Am I missing something? (I think I must be…)
1,2,3,4
How much do I love Feist? From the first song I heard of hers (Mushaboom) to the myriad others that followed, I was drawn to her haunting voice and her upbeat beat down sound.
And then, then, she comes out with this:
which is a take on this:
which is a feat almost surpassed by this:
and again, I could hear this song a million times and still not be sick of it. I’m in love.
PS. If you haven’t heard the Jack Penate cover of the song, go here or here and press the little play button. Addictive. Do I love it more than the original? Quite possibly. Another really good cover is by Bikini. And still another. Other amateur and not terrible covers: 1 2 3 4 (though I am thoroughly sickened by the t-shirt on the singer of cover 3).
The Supreme Court, Linear and Exponential Growth, and Racial Segregation
I just started reading Closed Chambers: The Rise, Fall, and Future of the Modern Supreme Court – and I came to an interesting case which could turn into a good problem dealing with exponential math.
A paraphrasing of the case
The case, originating in 1980, was filed by the U.S. Department of Justice and joined by the NAACP against the city of Yonkers, New York. The charge: violating the 1968 Fair Housing Act by purposely placing public housing in such a way as to perpetutation residential segregation. Finally, in 1985, the federal district court judge ruled in favor of the Department of Justice. However, with the ruling needed to come some sort of remedy — how could this wrong be righted?
The judge, Leonard Sand, ordered the city of Yonkers to build 200 public housing units spread throughout Yonkers, and to plan for subsidized housing in previously segregated neighborhoods. The city initially balked, but in January 1988, the city council formally agreed to the order. However, two weeks later, four of seven members of the city council decided to go back on their agreement, in defiance of the court.
Here’s where it gets interesting.
“Judge Sand first cajoled, then demanded, and finally threatened the city and its recalcitrant officials with contempt of course. As a last resort, Sand ruled that if the council did not adopt the necessary legislation by August 1, he would fine the city $100 a day, doubling every day until the legislation passed… In addition, he would fine each council member voting against the legislation $500 a day, with the possibility of incarceration after Day 10″ (page 40-41).
It wasn’t clear to me whether the fines would be cumulative or not (so if the fine after day 2 would be $200 or $200+$100), but from this New York Times article and others, I can say with a high degree of certainty that it was cumulative!
The fines were to start on August 2nd. However, they were suspended from August 9th to September 2th, while the case was waiting to be being heard by the appeals court and the supreme court.
The appeals court ruled that the exponentially increasing fine was excessive and unconstitutional. The ruling reads:
The City contends that the amount of the coercive fines imposed as a remedial sanction for civil contempt is excessive and a violation of the Due Process Clause of the Fifth Amendment and the Excessive Fines Clause of the Eighth Amendment. The fines start at $100 a day and double each day of continued noncompliance. As a result of doubling, the fine exceeds $100,000 for day 15, exceeds $1 million for day 21, and exceeds $1 billion for day 25.
Um… me thinks that even though it is a true statement that on day 15, the fine is more than $100,000, the justices probably meant day 11. Well, anyway, let’s continue:
The Court acted well within its discretion in starting the fine schedule at $100 a day. The Court also was entitled within reasonable limits to double the amount of the fine for each day of continued defiance. At that rate the cumulative fine after seven days, when we issued our stay, was $12,700. At some point, however, the doubling reaches unreasonable proportions. Under the current schedule the fine for day 25 is more than $1 billion; the fine for day 30 is more than $50 billion.
We believe that the doubling exceeds the bounds of the District Court’s discretion when the level of each day’s fine exceeds $1 million. The present schedule calls for a fine of more than $800,000 on day 14. We will therefore modify the contempt sanction against the City to provide that the fine shall be $1 million per day on day 15 and $1 million per day for every subsequent day of noncompliance.
So instead of having the fines double each day, after the doubling reached $1 million, each subsequent day, the fine would be another million bucks. The U.S. Supreme Court got the case in 1988 and decided not to grant a stay (meaning they didn’t want to put the Court of Appeals ruling on hold). In other words, the fines imposed by the Court of Appeals were constitutional and enforceable!
Even with the “reduced” fine, the city of Yonkers started to feel the pinch…
Mr. DeLuca [the city manager] has estimated that the city could pay fines through day 79, when the total would exceed the $66 million the city has in available resources… [NYT article].
On September 8, the New York Times ran an article about the drastic measures that Yonkers was about to be forced to take, since the contempt fines were nearing $1 million. By November 5th, the city would have to layoff 1,605 employees, leaving only 348 critical employees needed for minimal public safety and health! The article, rightly titled “‘Doomsday’ Layoffs Plan Adopted for Yonkers” continues:
According to the city schedule, ”all city services would be phased out after 12 weeks, on Thanksgiving Day, Nov. 24, 1988.” Under the state plan, the city would be operating under an emergency austerity program by Nov. 5, with the money saved available to ”retain a small work force” that would provide ”minimal public health and safety.”
Mr. DeLuca circulated a notice this evening to all employees, saying that they would be ”informed in writing as to your scheduled layoff date with as much notice as possible.” Employees would also be informed of their rights regarding unemployment insurance and options to continue benefit plans at their own cost.
”A final ‘Doomsday Plan’ will be in effect by Thursday morning,” Mr. DeLuca wrote. ”I regret to inform you this is not a rumor.”
Two days later, two of the four city council members who were defying the court order relented. The vote had switched, from 3-4 to 5-2. The first round of layoffs, scheduled in a matter of days, was averted.
Approval of the housing plan means an end to the fines that threatened to bankrupt the city, with the last assessment recorded on Thursday. The money already paid, $1.6 million in checks made out to the U.S. Treasury, will not be returned.
The case was not officially closed until May 2007 – twenty seven years after it began — when Judge Sand finally ruled that the court order had been followed through.
SOME MATH ANALYSIS
I made a graph of how much Yonkers owed the government each day starting on August 2nd until they agreed to the court order on September 9th:
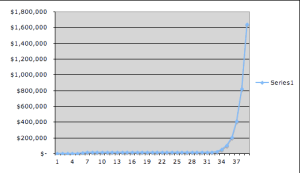
However, you can’t quite tell what’s going on for the first 30 days, because the scale is so large… And in general, when you’re plotting three or more orders of magnitude, you should plot on a log scale. So…
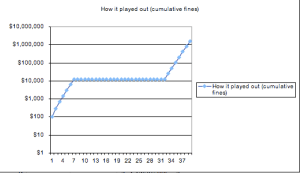
Notice the new scale (see the numbers on the left increase by an order of magnitude). It allows you to see more information. Like what’s that really long straight segment in the middle? Well, remember the fines were put on hold from August 9th to September 2nd, so the amount of money owed by Yonkers was kept constant for those days. That sort of “detail” got lost in the first graph, because the scale was so large!
And the first third of the graph looks linear, while it looked totally flat on the original non-log-scale graph. Why linear? Well, because remember the fines were doubling for all of those days, and when you plot exponential growth on a log scale, you get a line! But be careful! It isn’t exactly a line… We aren’t plotting $100, $200, $400, $800, etc., which would be perfectly exponential data. We are plotting the cumulative totals, which are $100, $300, $700, $1500, etc. These numbers don’t form a perfect exponential growth, though they are super duper close to being perfectly exponential! So for all intents and purposes, we can call it exponential, and hence, the first third of the graph is pretty darn linear. Since the last third of the graph still has the fines doubling and being added to the cumulative total, that section too is linear.
I also was really curious what would have happened if Yonkers didn’t pay up when they did… What if they let the fines accumulate until December 31st? Well, I also plotted that without and with a log scale…
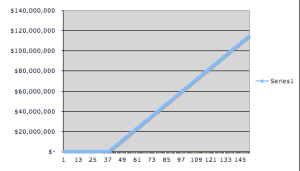
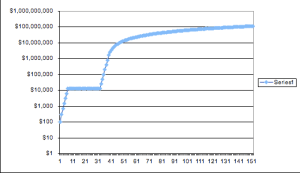
Looking at the first graph, we see that starting around day 37, we get a linear increase. Recall that’s because the Court of Appeals ruled that after the fines reached $1 million/day, they would stay $1 million/day. So each subsequent day, the fine just grows by the constant amount of $1 million.
(On the second graph, the log scale graph, we see the data go from linear to constant to linear — just like in our graph of what the town actually owed — but then the graph starts “slowing down” right at the same time the first graph becomes linear. That curve is actually logarithmic. Can you see why?)
My last hypothetical is: what if the Court of Appeals and the Supreme Court didn’t find the doubling fine unconstitutional. What would that graph look like if extended to December 31st? Plotted on a log scale, we get:
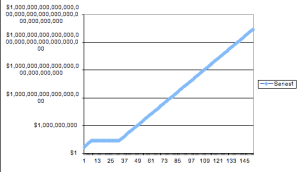
On December 31st, Yonkers would have owed the federal government: $17,014,118,346,046,900,000,000,000,000,000,000,000,000.
And as of the writing of this post, the national debt is only about $9,500,000,000,000.
YIKES! Good for the paying off the national deficit, bad for Yonkers.
A timeline for the case’s initial unfolding was published in the NYT here:
- Dec. 1, 1980: Justice Department sues Board of Education, City of Yonkers and Yonkers Community Development Agency, charging that the city racially discriminated in education and public housing.
- Dec. 1, 1980: Justice Department sues Board of Education, City of Yonkers and Yonkers Community Development Agency, charging that the city racially discriminated in education and public housing.
- Nov. 20, 1985: Judge Leonard B. Sand of Federal District Court in Manhattan rules that Yonkers’s housing and schools were intentionally segregated by race. A housing remedy order directs the city to build 200 units of public housing and to plan additional subsidized housing.
- Jan. 28, 1988: City Council approves consent decree that sets timetable for building 200 units of public housing and commits city to an additional 800 subsidized units.
- July 26: Court sets Aug. 1 deadline for Council to adopt zoning amendment needed to build the 800 units.
- Aug. 1: Council rejects amendment in a 4-to-3 vote.
- Aug. 2: Judge Sand finds city and the four Councilmen who voted against the amendment in contempt of court and imposes fines. The city’s fines start at $100 and double every day. The Councilmen are fined $500 a day.
- Aug. 9: The fines are suspended by a Federal appeals panel while the contempt ruling is appealed.
- Aug. 26: An appeals panel upholds contempt ruling and fines, but fines against the city are capped at $1 million a day. The fines remain suspended so the city can appeal to the United States Supreme Court. Sept. 1: The Supreme Court refuses to grant the city a further suspension of fines but does continue the stay of fines against the Councilmen so they can seek the High Court’s review of their contempt rulings.
- Sept. 2: Judge Sand reinstates the fines against the city.
- Sept. 5: Mayor Nicholas C. Wasicsko meets for 7 1/2 hours with the City Council in an effort to end the impasse, but no compromise is reached.
- Sept. 6: The Westchester District Attorney decides not to prosecute the four Councilmen who voted against the plan.
- Sept. 7: As contempt fines continue to build up, a state panel adopts a ”doomsday” plan to cut city services.
- Sept. 8: Fines pass the $1 million mark. As Yonkers residents confront layoffs and cuts in city services, pressure grows on the Mayor and the City Council to resolve the crisis. A City Council meeting over a transfer of funds to finance the fines erupts into a shouting match.
- Sept. 9: The City Council votes to accept the plan.
It’s Alive! Multivariable Calculus or Bust
As you might recall, I’m spending a chunk of this summer designing a multivariable calc course. The oft repeated phrase of the moment: GACK! This is a mini-challenge, because not only am I trying to plan out the curriculum, but I have to refresh my poor, atrophied brain which hasn’t touched “multi” (as I fondly nicknamed it) in forever. (Well, erm, 9 years, anyway.)
I spent yesterday searching the net for resources to have at my fingertips when designing the course. And to keep them all organized — in one place — I created a website to house it all.
My Multivariable Calculus Resource Webpage: multivariablecalculus.wordpress.com
I’m actually really proud of it, even though it’s still a work in progress. So if you have any interest, hop on by. Things of notice:
- Nine different free multivariable calc textbooks (!) are available online
- There are loads of great applets to visualize things like div, grad, curl, line and surface integrals, etc.
- There isn’t a set of free videos that I could find that go through major concepts in multivariable calc
- gnuplot is an incredibly powerful graphing utility
MIT, I’m disappointed in you
I love the MIT magazine Technology Review. This month’s issue had the following diagram in it, associated with an article about carbon footprints:
Anyone else see the problem? And anyone else see a teachable moment?
If you don’t see it, think about the data. You’re saying the World Average is 4 metric tons, the US Homeless Person is 8.5 metric tons, and US Resident is 20 metric tons. In any representation of the data, the US Homeless Person should be a bit less than twice the World Average. And the US Resident should be five times the world average.
Now look at the picture. Does that diagram represent that?
Put it another way: can you fit exactly five of the small circles in the largest circle?
(No.)
The diagram is misleading because you look at it and naturally compare areas. But unless you give it more than a glance, you won’t notice that the numbers (4.5, 8, 20) actually are the radii of the circles!
This could be the hook for a geometry or Algebra I class (on proportions, on circles, on data analysis). A teacher could then to parlay it to a discussion of how to “fix” the problem…
I see two easy solutions:
- Make a bar graph (boring solution)
- Make the same bubble graph, but make the radii
,
, and
respectively (more fun solution)
In coming up with the second solution, students will think about areas, proportions, and visual representations of data. I can see students each approaching and solving the problem slightly differently, but still getting the same answer. In that sense, it allows for some grappling and struggle.
I still love the Technology Review. Not only is it full of good reads, but good ideas for lessons!
Look below the jump for a revised graph, which accurately represents the data…
A challenge for my students; or, laying down the gauntlet
This is too good not to use in the classroom… mwa hahahaha. (Found via Digg: here)
A simplistic explanation (which is all I wanted) is here:
Your brain can make your hand write a 6 in the normal direction no problem at all, and it can circle your foot in a clockwise direction, no problem at all either. But when you try to do both types of movement at the same time, big problems.
This is because your brain now has to send very different movement instructions to your arm and leg together at the same time. Your brain is simply not used to doing different things with your arm and leg at the same time in this way.
Note: another one is to “try to simultaneously rotate the index fingers of both hands in the same direction (clockwise or anticlockwise). Do it slowly at first, then faster, and faster…. Pretty soon, they’re going in opposite directions.” (from metafilter)
Math History on the Net
arXiv.org was originally designed to be a repository for pre-prints of physics articles, but it has since been expanded to other disciplines. I recently discovered that even though most of the math pre-prints are out of my league, there is one category of math articles that I have a good chance of understand: math history.
So if you want to explore mathematicians writing the history of mathematics, go here. (I found an interesting article on the solution of the Poincare conjecture in this haystack.)
The former historian in me has to point out, however, that for the most part, mathematicians writing history (of mathematics) is fascinating for the general “we are interested in math” audience. But historians will cringe at the teleology and absence of any culture in these narratives; they tend to be self-contained, internalist, and lack nearly everything that historians value in their craft.
There are really good historical works on mathematics written by mathematicians, I’m sure. But I guess I want to say that there are really good historical works on mathematics written by historians too. I would argue — from what little I’ve read in both realms — that these works by historians are often better, more considered, and more interesting. And the really good ones don’t skimp on the mathematics either, but delve deep into the mathematics, and relate the mathematics to culture.
A few from the top of my head:
Karl Pearson: The Scientific Life in the Statistical Age (Ted Porter)
Masters of Theory: Cambridge and the Rise of Mathematical Physics (Andrew Warwick)
Mechanizing Proof: Computing, Risk, and Trust (Donald MacKenzie)*
*Actually, this is a sociology of mathematics book.
Cultural Anthropology in High School
Today I had yet another idea I had for a classroom that isn’t my own. It’s a bit of a long-winded post, so just look after the jump if the subject line intrigues you.
Help? Multivariable Calculus!
I need help! GACK!
So I’ve decided that my one week of lazing about and reading (finished Middlesex and the teen novel It’s Kind of A Funny Story, and started Heat) is officially over [1]. It’s time to get to work!
A mere two hours ago, I hoisted the Multivariable Calc book that I’ll be teaching from next year from the pile on the floor to my desk and gave it my first run through. It looks okay [2].
I’m designing this course from scratch, and I wanted to ask for some advice for anyone who has taught it, or has ever designed a course from scratch…
- Anything — print or web resources, jokes, songs, videos, pictures? Also, it doesn’t have to be about multivariable calculus; any advice on how to design a really awesome course from scratch would be much appreciated! How long did it take you, what resources did you draw upon, did you make a general outline of topics or a specific day-by-day schedule, did you write your assessments beforehand or during the school year once you’ve gauged the students’ abilities, and the other million questions that I’m thinking of.
- Does you know of any good software for graphing in 3-D that is open source (read: free) and works on a PC? I know of SAGE, and OCTAVE, and the like, but I’m wondering if those programs are a bit overkill for this course. Is there something less bulky out there? Maybe even a really powerful 3-D graphing calculator that people like?
UPDATE: I just remembered that SAGE came out with the online SAGE notebook, which is what I think I’ll probably implement! It’s like MAPLE in terms of the command line, and it seems extraordinarily powerful.
- How do you teach your students to graph in 3-D by hand? How do you do it on the board? SmartBoard?
- Have you ever taught a class with 3-5 students before? Do you treat it like a regular class — with lecturing but with more individualized attention? Or did you teach it seminar style? What would a seminar style math class look like?
- Do you have any good investigative activities or projects for multivariable calc? Or that you do in calc that can be extended?
- Have you ever just thrown out teaching from a textbook and used an online textbook? Or mixed and matched textbooks? Or taught without any book?
Hopefully I’ll use this blog to post about the evolution of the course design as the summer progresses… so don’t change that RSS reader!
[1] Other books that are lined up to be read this summer are Fight Club, The Kite Runner, and The Adventures of Huckleberry Finn (all for school); if I have time, I also want to read Lazarus’ Closed Chambers, Tartt’s The Little Friend, Dewey’s The School and Society and The Child and the Curriculum, Pais’ The Science and the Life of Albert Einstein, and finish up the second half of Gogol’s Dead Souls.
[2] I’m using Anton’s Calculus, Early Transcendentals, 8th Edition. My school uses the first half of the book in calc classes and I don’t want to make my students buy a second book. My initial opinion: the book is okay but seems to be unnecessarily dense in places, and could have left a number of sections out. The exercises at the end of each section are quite good.
Actual good math humor. Seriously. I’m not kidding.
Update: I discovered a new comic site (abstruse goose) that I like almost as much as xkcd… it’s more ribald and there are a number I could never show my students. Which is a good thing! An example below:
Update 2: xkcd has a forum with math jokes.
