Yesterday I ahem-ed and winked to my Algebra II class about them needing to know how to complete the square for class today. Teaching this topic last year was a nightmare. A total trainwreck. Students were having difficulty all over the place — they couldn’t simplify radicals, they didn’t get why the procedure worked, they were wondering how imaginary numbers came into play here, they confused the steps, they didn’t *get* it. And it was my fault.
Part of the problem was that we were doing too much, too fast. We had brought in graphing quadratics early on, and we were emphasizing the relationship between the equations and the graphs from the start. We also — in the middle of the quadratic unit — taught complex numbers. That’s too many huge things to deal with. Quadratics bring too much together, and we needed to keep the ideas and skills organized so they make sense.
So the other Algebra II teacher and I decided we’d try something different. First, this year, we introduced complex numbers without talking about quadratics. We motivated these numbers, and then we had students practice working with them, getting really comfortable with them. Second, when we started quadratics, we did so without any graphing. Period. We were doing all algebraic work.
Here’s how we progressed.
PART I: Review
Regular, very simple equations with solutions involving square roots, imaginary numbers, and real numbers:

Quick review of factoring:

A brief discussion of solving equations with perfect square terms — with imaginary and real solutions:

Part II: Completing the Square
Perfect Squares:

We talked about what a perfect square is and noticed a relationship between the four terms — when you FOIL. Importantly, students are going to see that the second and third terms are the same.
***
Creating Perfect Squares!:

The next step of creating perfect squares really has them grapple with the fact that the missing constant term is simply half of the coefficient of the  term squared.
term squared.
***
Completing the Square:

For me, it was this step, just a short distance from the last step, which made the entire unit a success. Because now my students had seen the relationship between all the terms in a perfect square and actually seemed to understand them. My favorite part was that most students were getting problem 10 right — and it involves fractions! We also talked about how important signs are for this process.
***
The End Game: Completing the Square
Before we actually “completed the square” I had students look at the last section of the review sheet.

We talked about how if you can write a problem in this form, that you can ALWAYS solve it. And what we were going to be doing is finding a way to write any quadratic equation in that form, so we can solve it.
Then, I went through an example — step by step — to get a problem to that form:

Then I had them solve it, like they had done previously. Most of them had no trouble solving it.

They practiced doing a few problems on their own — some which gave “nice” answers, some which gave answers with radicals, and some which gave complex answers.
Part III: Reinforcement
I made them practice a few more times, with some harder problems, and then I threw them a curve ball — a coefficient in front of the 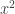 term. We conquered that, although there were same difficulties with fractions. Then I put some terms on one side and some terms on the other side (e.g.
term. We conquered that, although there were same difficulties with fractions. Then I put some terms on one side and some terms on the other side (e.g.  ).
).
Overall, they really rocked it. How do I know they got it?
I started off this post by saying that I ahem-ed about giving a pop quiz in my class today. Well, I followed through on that. gave a pop quiz to my class on completing the square. I gave them one easy problem and one much more difficult problem — with fractions and radicals — on completing the square.
I got a whole bunch of perfect scores.
If you want, the worksheets I created are below:
Factoring Quadratics
Completing the Square, Part I
Completing the Square, Part II
Completing the Square, Pop Quiz
. When I plot the data (pink) and the exponential line of best fit (blue) on the log-scale graph, you’ll see that Moore’s Law looks like it has some serious bite to it.












