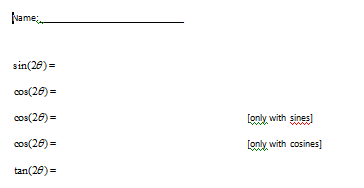What are the ways we can generate ellipses?

We’ve been working with ellipses. I have talked about some of these this year. Others I haven’t. But I like this list for future reference.

• The polar equation gives rise to ellipses if
  
• An ellipse arises out of squashing or stretching a unit circle horizontally or vertically (or both)
  which means that algebraically…the rectangular equation is

• An ellipse arises out of looking at a circle straight on (so it looks like a circle) and then tilting that circle.

• Ellipses can be created by taking a cone (or cylinder) and slicing it at a variety of anglesThis is equivalent to shining a flashlight at a wall at an angle:

• The set of points from two points (called foci) which have a set sum of distances from these two pointsand for a cool video illustrating this (alongside the reflective property of ellipses):
• Drop a planet in space near a massive object, and give it an initial push (velocity)
  [not drawn to scale, obvi.]

One Ring Equation to Rule Them All

On Monday, in Precalculus, I am starting conic sections.

I’ve made the decision to introduce conics through polar equations. This is totally backwards to the way that most people do it. Our textbook even sticks the polar version of conics at the end of the chapter of conics. However, I think it will be more powerful to do it this way.

You see, we just finished a unit on polar a hot minute ago, and I want to capitalize on that so students can draw connections between polar and conics. Additionally, we did a project on families of curves.

And in case you didn’t know this, the polar equation [1] give rise to all the conic sections by varying the parameter . In other words, you can see all conics as a family of curves with a varying parameter.

Noticing and Wondering

For you, I decided to take a few seconds to plot them on geogebra:

Instead of teaching them anything, on the first day I’m going to have them work in pairs. The plan:

• Have students get in pairs
• Have students use desmos.com to explore the family of curves using a slider to change
• Have each pair notice things and wonder things about what they see as they change the parameter — and record their observations on a google doc (this sample doc is set so you can view it)
• After each pair is done noticing and wondering about , I’m going to have kids spend a few minutes noticing and wondering about 

I’m handing out this worksheet [.docx] to get us to do these things.

I don’t know how long this will take. Maybe 20 minutes, maybe 50 minutes? It really depends on how into the noticing and wondering. I’m a little uncertain where to go next with this — how to share the noticing and wondering… Each pair is going to have a group letter (A, B, C, … H, I, J). So I might have them spend a few minutes looking at the documents of those that preceed and follow their group (e.g. C will look at group B and D’s group’s observation).

Then I’m not sure how to wrap this all up. I think what I may do is leave it there, and not do a whole-class share. But after that, I’ll collate their noticings and wonderings, and as we introduce new things, I’ll tie them back to statements from these documents. For example, if a group notices “when is a huge number, the graph looks like two intersecting lines,” when we get to hyperbolas, I’ll start the day reading that statement, and after delving into them, we’ll return back to that statement to see how it relates to the algebraic work we did. Or if a group wonders, “When , I wonder if there’s a relationship between the value of and the angle between the two intersecting lines,” I could build that into the questions in the worksheets I’m writing for this unit.

Or maybe I’ll do nothing with them. Just the mere act of exploring, and coming with the conclusion that one family of polar curves can general four distinct general shapes (circle, ellipse, parabola, hyperbola) is good enough for me. Just paying attention to what’s happening to the graph, and learning to ask questions about what’s happening, that’s a skill in itself I should be content with cultivating.

(I should point out that I have rarely used the notice/wonder thing… so this isn’t fluent for my kids.)

Where I go from Here

From this activity, though, we are definitely going to talk about how we see four qualitatively distinct shapes, and we’ll name them:

circle, ellipse, parabola, hyperbola

And since we aren’t relying too much on the textbook, I am going to want them to make a schematic chart to organize what they’ve uncovered through observation.

And then we go on to the icky algebra, identifying various polar equations as different types of conics, and then eventually converting polar to rectangular form. (But in our polar unit, they already were asked to convert equations like to rectangular coordinates, so this will be a bit of review.)

[.docx]

This is all subject to change, obviously.

And then… then… when students have qualitatively understood conics as all emerging through one equation… when students see that the conics all gently slide into and out of each other as a single parameter changes… when students see two things they already know (parabolas and circles) and see two things they don’t know (ovals, weird pairs of curves that look almost like crossing lines)… then we’ve motivated this luscious mathematical journey we’re going to embark on. [2]

Then we can get to the rectangular form for conics and see how they come to look so similar, and why the differences arises… Why certain things open up and certain things open sideways… all the traditional stuff… But motivated by this untraditional beginning.

UPDATE: It’s Sunday, before I try this on Monday. I decided I want kids to understand why hyperbolas have asymptotic behavior from the polar form (and why ellipses don’t!). So I made this sheet [scribd online, .docx] which I think will get them to discover some algebraic connections behind some of the visual things they will have uncovered from their noticing and wondering.

UPDATE 2: My kids did their noticing and wondering. Because they were comfortable with Desmos from our polar unit, it went really smoothly. It took them about 25 or 30 minutes before they had exhausted all their observations. I walked around and pressed a few on some of the things they were doing/saying without giving anything away… Like if they said when that the graph is a parabola, I had them graph to confirm that it wasn’t… and then they had to zoom out to see it truly was an ellipse. Or if they said that very high values of give rise to intersecting lines, I would ask them to record in their noticings the point of intersection was (so they’d zoom in and see there was no point of intersection!). All my kids’s observations are recorded here in their google docs: Group A, B, C, D, E, F, G, H

 

[1] And, technically, 

[2] I’m in the middle of Paul Lockhart’s Measurement and what’s amazing is I was reading it on the subway to school, and today of all days, I started his introduction to conics. He introduces it in a stunning way, through projections, and showed me one of the most elegant proofs I’ve seen dealing with ellipses and why the sum of the distances from the foci to the ellipse is a constant. I wish I could move away from our traditional curriculum to work as qualitatively and beautifully as he has done.

I have now printed out my Families of Curves projects at school, and hung them up. I still have to look through the actual booklets that students turned in and give feedback, but the actual way that these look — once hung — is pretty awesome.

I used just some tags I had lying around (I love buying random useless stuff from Staples and hoarding it at my desk at school) and dissection pins. I photocopied their artwork on cardstock.

Being honest, I hung them because I wanted the kids to think “Hey, Mr. Shah liked these enough to take the time to do this.” Implicitly. I wanted the kids to know I was proud of their creations (and to let them know that they should be proud of them too.) No kid in my class has said “Hey, that’s awesome.” So I don’t know if I accomplished that goal. But I have heard a zillion other people say how much they have liked seeing them there. A number of other teachers have randomly come up to me unsolicited to tell me how cool they think they are. And the head of the Upper School gave them a shout out in the Upper School meeting. And just recently, yesterday at the subway, I ran into a student who graduated a couple years ago. And she was at our school because her brother goes here, and she said she was looking at them thinking “how cool! Mr. Shah!”

Another great moment with these was having two of my kids go to a neighboring school which holds a math art seminar, and watch these kids talk with other students about their work. It was clear how invested these two kids were. Watching them articulate their process just made my heart melt.

[Here is Families of Curves #1, and Families of Curves #2]

After my last unit, which didn’t go as well as I’d have liked, I have been teaching a unit on polar. Where one space (rectangular) transmogrifies into another space (polar).

I’ve been content with what the kids have done this unit. Again, they did all the discovery.

• How to change a point in rectangular coordinates to polar
• How to change a point in polar to rectangular
• How to graph a polar point — and find a bunch of different ways to represent that point in polar coordinates (showing that polar coordinates are not unique, unlike rectangular coordinates)
• How to convert from a rectangular equation to the polar equation
• How to convert from a polar equation to a rectangular equation
• How to graph simple polar equations by hand
• How to conceptually understand what the polar graphs will look like, and why
• How to graph complex numbers on the complex plane
• How to represent complex numbers in polar form (“cis”)
• How to multiply and divide complex numbers using polar form
• How to take find roots of unity (haven’t taught yet… throwing it in tomorrow…)

This unit, I’ve been more conscientious about collecting their work almost each night, so I could see their problems. One big thing was that I identified that rectangular points in the 2nd and 3rd quadrants provided difficulty when converting to polar (because of the inverse tangent function, which only yields angles in the 1st and 4th quadrant). Because of that, I was able to target that and bring that up in class, and incorporate more points there.

I think I made some solid — but very basic — materials for polar. I’m going to share them below, and explain each one of them…  [In Word format, in case you want to use/modify them, they are here: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10]

1. Introduction to a new space: This is my introduction to polar. I introduce the idea of isotropy (without using the word) and say that we need things to anchor us so we can refer to them. One way — the way we’ve always done it — is using how for north/south we’ve gone from the origin, and how far east/west we’ve gone from the origin. Our regular rectangular coordinates. But… BUT there is another way. I have them play a few rounds of polar battleship on Geogebra to get a sense of it, without telling them anything. Then, without any direct instruction, students move on to actually convert from rectangular coordinates to polar. I do a little direct instruction about how to plot polar coordinates, when is negative and when is negative. And then they do some plotting, and then convert from polar coordinates to rectangular coordinates. Most importantly, they figure out how to do these conversions on their own. 

2. Graphing in Polar: The warm up refreshes kids on the equation for a circle, but it also importantly has them graph a horizontal and a vertical line. When we talk about the warm up, I really emphasize that for the equation , what does that mean about the coordinate? (“It can be ANYTHING! There is no restriction placed on !”) The reason this is so important is that when they graph , I hope they say “well is stuck at , but the angle can be anything” (and similarly, for , “I suppose is stuck at , but can be anything.”). The rest is pretty much saying: okay, we’ve got our conversions for individual points… can we use them to convert whole equations? (Yes.)

3. Understanding Polar Graphs: Now, after all of this, we’re finally going to graph our first not-so-simple polar equation by hand. We do the very basic first one together, and then they’re off to the races! I wasn’t sure how much I truly cared about them graphing by hand, but it’s clear to me now that doing a few of these by hand really brings to life what graphing in polar truly means. Especially when you get negative r values.

4. Polar Graphing Exploration: This was a day and a half of conceptual lifting, done by the students. There is the most amazing polar applet created by David Little. More than anything else, this one applet has truly let me understand how polar graphs are created. It’s simple, and amazing. I didn’t want to teach my kids about the different names for the different graphs, and to identify what the graph will look like based on the equation. Instead, I wanted them to be able to understand why some graphs have a dent, why some look like a  loop with a loop-de-loop inside of it, why some are spirals, and why some are flowers.

So I had them use the applet — and the packet — to explore. And I have to say: they were really making solid connections, and having good conversations, as they were going through it. If you use it, the one thing you want to tell the kids is to “not touch a” and “after you finish analyzing one graph, change b back to b=0.1$”. Honestly, this was the most “risky” of my classes because instead of staying traditional, I said “here, learn it.”

5. Shape of a Polar Graph: After they finished their exploration, I wanted to see what they took away from it, so I gave this out. I collected it and read through them. Some kids fared better on it than others. I didn’t have time to mark them up and give lots of individual feedback, so instead I created a solution packet and I gave it to them — letting them compare, ask questions, etc.

6. Polar Practice: After the last assessment, because I wasn’t totally confident on my kids’s ability to do the basic types of problems, I whipped this set of problems up, which I gave to them, collected, and harshly marked up. This was the best feedback for me, because I got to see what kids were confident about, and what they struggled with.

7. Complex Numbers, the Complex Plane, and Polar Coordinates: I start bringing complex numbers into the mix. I first have them spend a few minutes trying to multiply and divide complex numbers, but it starts getting tedious and annoying (it’s supposed to). We talk about what a complex plane looks like, how I can graph complex numbers on them, and how complex numbers not only have a rectangular (a+bi) form, but also a polar form (involving and ). They don’t seem to have any trouble getting that.

Then: BAM! I immediately have them do a problem, look for a pattern, and make a conjecture. The theorem we’re going for says that if you have two complex numbers written in polar form, if you multiply these numbers, you simply have to multiply the values and add the values. BAM. Awesome. So they see this. We talk about whether it’s a proof or not (it’s not). We talk about another example to evidence it, and then I let them loose on complex multiplication and division problems.

8. Basic Practice Problems for Complex Numbers: These are the practice problems I gave for students to work on. I also taught them how to use their calculators to input, store, and multiply/divide complex numbers.

9. Advanced Practice with Complex Numbers: This is a short sheet that has kids prove DeMoivre’s theorem.

10. Complex Roots:  I wanted to teach roots of unity, but I don’t have a lot of time, so I made this sheet up — and we’re going to walk through it together. (Tomorrow.) We almost never do that. But it’s our last class before the test, and I think it’s just so cool that I have to show it to them.

Reflecting back, I feel kinda bad that I didn’t design this sheet backwards. Start by having students draw a perfect, regular pentagon on the coordinate plane (letting one point be (1,0) and the center at (0.0)). Then have them find the coordinate of the vertices of the pentagon. Then talking through the vertices to conclude they all are roots of unity (if we consider the plane a complex plane). But eh, I didn’t.

So today I had this experience where this precalculus test I gave was a bit of a bloodbath. Not for everyone, but for more than usual. In a way where I cringe, cry out to the high heavens, and scream:

WHYYYYYYYYYYYYYYYYYYYYYY?

The reason is because I felt pretty proud of the way I have been introducing the material. You see, in precalculus this year, the kids are coming up with everything on their own. I don’t give them anything.* And thus far they’ve been doing well with this. And during this unit, even though I didn’t quite have the same amount of time to create everything to my best ability (I relied a lot on the textbook for this stuff), I felt pretty confident about my kids’s understanding.

So I have to wonder: Where did I go wrong as a teacher? What was different about this unit than the others?

First off, this unit was some pretty heavy stuff. We were deriving and applying the trig formulas, and then we were solving more complicated trig equations (they had done basic trig equations previously). All in all, we took a total of 8 days to do this. I should also note that this is an advanced class, and they have been doing a lot of collaborative work this year.

FYI: these were the trig formulas we derived and applied… this is the “trig formula family tree” I made for them.

And for this unit, I led class in a pretty routine way. Each day I had a packet for the kids to work on. They would work on the warm ups with their groups (which were designed to activate prior things they knew but forgot, and have kids make some connections on their own). After 5-10 minutes, we would all talk through the warmup problems together.

Then I would let each group work on their own. I would walk around and facilitate, nudge, question, and answer questions. On some packets, I would have special places where I told kids to “draw in a heart, and call me over when you get to the heart.” (But to be honest, overall, I think I was throwing myself into the groups less than I usually do this unit, as I’ve been trying to let go.)

Then class would end. Most groups were where they should have been… close to done with the packet, and ready to start working on the book problems. These book problems varied in difficulty from the routine “can you do something simple?” to the “okay, apply this in a moderately deep way.” For this unit, I did assign more nightly work than I normally assign, because I knew that to get good at this stuff involves a lot of practice. (I don’t think that is true for everything in math, btdubs.)

Then at the start of the next class, I would have one set of my handwritten solutions per each table (that way, three kids have to share, and thus talk!). I would give kids 5-10 minutes to compare their answers, talk with their groups to figure out things they were doing wrong, and then we would come together as a class and I would field questions that groups couldn’t answer. Then we started a new packet, and the process continued like that for most days. [We did have a bit where we did a paper folding activity, which was pretty cool.]

To see what these packets look like, I combined all of them here so you can scroll through them. I highlighted some of the problems/questions which I thought were good at getting at something hard/interesting/conceptual:

As you can see, these aren’t really great. Not bad either, though. [1]

So where did things go wrong?

When I look through the tests, here are some things I noticed as a trend:

• Kids struggled with some of the basic “apply the formula” questions
• Kids had trouble figuring out which sign to use when using the half angle formulas (e.g. 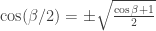) [2]
• Kids really nailed the conceptual explanation part of “how many solutions does this trig equation (e.g. ) have on the interval $\latex 0\leq\theta<2\pi$?” question
• Kids struggled with remembering that when you take the square root of both sides, you get two solutions (so is really two equations to solve)
• Kids did a pretty good job of deriving the trig formulas
• Even though kids did a pretty good job on the “how many solutions does this trig equation have?” they didn’t find all the solutions to the basic trig equations given.

As far as I can tell, here were the contributing factors (in no particular order):

(a) Lots and lots of sickness. I still have 5 kids who haven’t taken it (out of 19).

(b) I thought I was getting formative feedback when I gave regular little mini non-graded “do you remember the trig formulas we’ve derived” at the start of some classes…

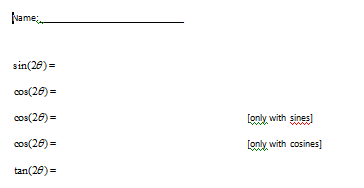
And honestly, I felt proud that I have been making a conscious effort to collect this formative feedback. But now I see it wasn’t the right formative feedback.

(c) I usually get a good amount of formative feedback in Precalculus. Mainly I do it by collecting of the nightly work, marking it up, and handing it back. Thus I usually know what students are understanding and what they are not, and they also know what they understand and what they don’t. However, because I was swamped, I didn’t really do that. Maybe once in eight days? So each day, kids got to compare their own work to my solutions, which I thought would at least give THEM feedback… But I never got to see what kinds of mistakes they were making, or where they were getting tripped up, not in detail and not in a big-picture way. So I didn’t build these things into the lessons… which is important because…

(d) This material is hard. Harder than some of the previous units/ideas. That’s because this unit required conceptual understanding, juggling a lot of memorized formulas, a bunch of intuition (as to how to start solving the trig equations), and a lot of “fact” information (like where in the unit circle is ?). It’s just pulling a lot of stuff together.

(e) I should have spent more time reminding them of the trig equations they had previously solved. I assumed that they remembered all of that stuff we did weeks ago and could apply it. I jumped in too fast.

(f) The test was a bit too long. The kicker is, I thought it was too long, so I cut some stuff out. I was trying to be conscious of that. Well, the road to hell…

So there we are. Surprisingly, typing this out has made me feel a lot better. I feel like I now have a better grasp on why something I thought was going pretty well was actually not going as well as I thought. I also have some concrete ideas on what to do next year. The main takeaways for me are: go slower, bring in more visual understanding for trig equations, don’t mess around with the harder stuff, get a lot of formative feedback on the basic types of problems, and make the assessment shorter than my intuition tells me.

*Okay, to be fair, I have given them two things — one which we proved later, the other which I never proved. (The former was the sum of angles formula for sine and cosine, the latter was Heron’s formula.)

[1] It was a stressful time when I was doing this unit, and so I just didn’t have time to come up with anything better. But still, I think they get at good stuff. Even if there needs to be A LOT MORE GRAPHING next year. We did a lot of graphing when we did basic trig equations. We should have done graphing here too.

[2] The kicker is that I said in class that figuring out the correct sign is the most important thing about applying that formula. Multiple times. But me saying it until I’m blue in the face the same as them totally understanding it. Next year I need to build in some warm up questions like: if , what quadrant is in? Draw a picture. If is in the fourth quadrant, explain in words and with pictures why is in the second quadrant..

I’m sure that this question has been asked in a million high school math offices, so apologies for the rudimentary nature of the question.

I’m teaching Precalculus for the first time. And I’m about to teach proving trig identities, like:

I understand that the standard ways to prove trig identities is:

(a) pick one side of the equation, and keep morphing it until it matches the second side of the equation

(b) individually modify both side of the equations independently until they equal the same thing.

I always learned that what you cannot do is start mixing both sides of the equations. So, for the equation above, you can’t cross multiply to get:

and keep on simplifying both sides to show they are the same and the equality is true.

 

The reasons I’ve heard this is not allowed:

1. Because I said so.

2. You can only cross multiply if you know the equality is true. But that’s precisely what you’re trying to prove. You are assuming the statement is true to prove the statement is true.

However, both explanations are unsatisfying to me. The first one is for obvious reasons. My objection with the second one is that it seems to always work for these problems. Although I know it is logically unsound, I can’t quite pinpoint why with a concrete example to demonstrate it.. 

My questions are the following:

What do you do to explain to your kids why you can only work the sides of the equality independently? Does it convince them?

Does anyone have a good example involving trigonometric identities that illustrates that bad things happen when you don’t solve the sides independently, but start mixing them together? Like proving something that isn’t true actually is true… or proving something true that actually isn’t true?

Thanks for any help. I feel a little foolish, like I’m missing something obvious. Like I should know this. But hey, if I knew everything, I wouldn’t need all y’all.